题目内容
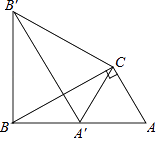
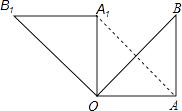
【题目】如图,在Rt△OAB中,∠OAB=90°,OA=AB=6,将△OAB绕点O沿逆时针方向旋转90°得到△OA1B1 . 
(1)线段OA1的长是 , ∠AOB1的度数是;
(2)连接AA1 , 求证:四边形OAA1B1是平行四边形;
(3)求点B旋转到点B1的位置所经过的路线的长.
【答案】
(1)6;135°
(2)证明:∵∠AOA1=∠OA1B1=90°,
∴OA∥A1B1,
又OA=AB=A1B1,
∴四边形OAA1B1是平行四边形
(3)解:L= ![]() =3
=3 ![]() π
π
【解析】(1)解:因为,∠OAB=90°,OA=AB,
所以,△OAB为等腰直角三角形,即∠AOB=45°,
根据旋转的性质,对应点到旋转中心的距离相等,即OA1=OA=6,
对应角∠A1OB1=∠AOB=45°,旋转角∠AOA1=90°,
所以,∠AOB1的度数是90°+45°=135°.
【考点精析】利用平行四边形的判定和弧长计算公式对题目进行判断即可得到答案,需要熟知两组对边分别平行的四边形是平行四边形:两组对边分别相等的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;两组对角分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形;若设⊙O半径为R,n°的圆心角所对的弧长为l,则l=nπr/180;注意:在应用弧长公式进行计算时,要注意公式中n的意义.n表示1°圆心角的倍数,它是不带单位的.

 名校课堂系列答案
名校课堂系列答案【题目】二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如表
x | ﹣1 | 0 | 1 | 3 |
y | ﹣1 | 3 | 5 | 3 |
下列结论:
①ac<0;
②当x>1时,y的值随x值的增大而减小.
③3是方程ax2+(b﹣1)x+c=0的一个根;
④当﹣1<x<3时,ax2+(b﹣1)x+c>0.
其中正确的结论是 .