题目内容
【题目】如图,在△ABC中,∠ACB=90°,AC=1,将△ABC绕点C顺时针旋转60°至△A′B′C,点A的对应点A′恰好落在AB上,求BB′的长. 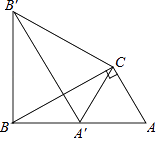
【答案】解:∵将△ABC绕点C顺时针旋转60°至△A′B′C,
∴CA=CA′,CB=CB′,∠ACA′=∠BCB′=60°,
∴△ACA′和△BCB′均为等边三角形,
∴BB′=BC,∠A=60°,∠CBB′=60°,
∵点A′在AB上,∠ACB=90°,
∴∠A=60°,∠ABC=90°﹣∠A=30°,
在Rt△ABC中,BC= ![]() CA=
CA= ![]() ,
,
∴BB′= ![]()
【解析】先利用旋转的性质得CA=CA′,CB=CB′,∠ACA′=∠BCB′=60°,则可判断△ACA′和△BCB′均为等边三角形,于是得到BB′=BC,∠A=60°,∠CBB′=60°,接着计算出∠ABC=90°﹣∠A=30°,则可计算出BC的长,从而得到BB′的长.
【考点精析】利用旋转的性质对题目进行判断即可得到答案,需要熟知①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
【题目】为了帮助市内一名患“白血病”的中学生,东营市某学校数学社团15名同学积极捐款,捐款情况如下表所示,下列说法正确的是( )
捐款数额 | 10 | 20 | 30 | 50 | 100 |
人数 | 2 | 4 | 5 | 3 | 1 |
A. 众数是100 B. 中位数是30 C. 极差是20 D. 平均数是30