题目内容
【题目】阅读下列材料:
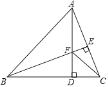
(材料)如图,对任意符合条件的直角三角形BAC,绕其锐角顶点逆时针旋转90°得△DAE,所以∠BAE=90°,且四边形ACFD是一个正方形,它的面积和四边形ABFE面积相等,而四边形ABFE面积等于Rt△BAE和Rt△BFE的面积之和,根据图形我们就能证明勾股定理: ![]() .
.

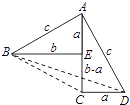
(请回答)如图是任意符合条件的两个全等的Rt△BEA和Rt△ACD拼成的,你能根据图示再写一种证明勾股定理的方法吗?
【答案】详见解析.
【解析】
根据△ABC和Rt△ACD的面积之和=Rt△ABD和△BCD的面积之和求解即可.
此图也可以看成Rt△BEA绕其直角顶点顺时针旋转90°,再向下平移得到.一方面,四边形ABCD的面积等于△ABC和Rt△ACD的面积之和,另一方面,四边形ABCD的面积等于Rt△ABD和△BCD的面积之和,
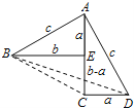
所以:![]()
即:![]()
整理:![]()
所以:![]()

练习册系列答案
相关题目