题目内容
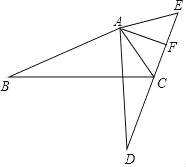
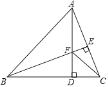
【题目】如图,在△ABC中,∠ABC=45°,AD,BE分别为BC、AC边上的高,AD、BE相交于点F,连接CF,则下列结论:①BF=AC; ②∠FCD=45°; ③若BF=2EC,则△FDC周长等于AB的长;其中正确的有( )
A. 0个 B. 1个 C. 2个 D. 3个
【答案】D
【解析】
证明△ADC≌△BDF即可一一判断.
解:∵△ABC中,AD,BE分别为BC、AC边上的高,∠ABC=45°,
∴AD=BD,∠DAC和∠FBD都是∠ACD的余角,
而∠ADB=∠ADC=90°,
∴△BDF≌△ADC,
∴BF=AC,故①正确,
∴FD=CD,
∴∠FCD=∠CFD=45°,故②正确;
若BF=2EC,根据①得BF=AC,
∴AC=2EC,
即E为AC的中点,
∴BE为线段AC的垂直平分线,
∴AF=CF,BA=BC,
∴AB=BD+CD=AD+CD=AF+DF+CD=CF+DF+CD,
即△FDC周长等于AB的长,故③正确.
故选:D.

练习册系列答案
相关题目
【题目】小明购买了一部新手机,到某通讯公司咨询移动电话资费情况,准备办理入网手续,该通讯公司工作人员向他介绍两种不同的资费方案:
方案代号 | 月租费(元) | 免费时间(分) | 超过免费时间的通话费(元/分) |
一 | 10 | 0 | 0.20 |
二 | 30 | 80 | 0.15 |
(1)分别写出方案一、二中,月话费(月租费与通话费的总和)y(单位:元)与通话时间x(单位:分)的函数关系式;
(2)画出(1)中两个函数的图象;
(3)若小明月通话时间为200分钟左右,他应该选择哪种资费方案最省钱.