题目内容
【题目】如图,AB是大半圆O的直径,AO是小半圆M的直径,点P是大半圆O上一点,PA与小半圆M交于点C,过点C作CD⊥OP于点D. 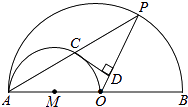
(1)求证:CD是小半圆M的切线;
(2)若AB=8,点P在大半圆O上运动(点P不与A,B两点重合),设PD=x,CD2=y. ①求y与x之间的函数关系式,并写出自变量x的取值范围;
②当y=3时,求P,M两点之间的距离.
【答案】
(1)解:连接CO、CM,如图1所示.
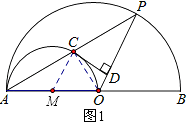
∵AO是小半圆M的直径,
∴∠ACO=90°即CO⊥AP.
∵OA=OP,
∴AC=PC.
∵AM=OM,
∴CM∥PO.
∴∠MCD=∠PDC.
∵CD⊥OP,
∴∠PDC=90°.
∴∠MCD=90°,即CD⊥CM.
∵CD经过半径CM的外端C,且CD⊥CM,
∴直线CD是小半圆M的切线
(2)解:①∵CO⊥AP,CD⊥OP,
∴∠OCP=∠ODC=∠CDP=90°.
∴∠OCD=90°﹣∠DCP=∠P.
∴△ODC∽△CDP.
∴ ![]() .
.
∴CD2=DPOD.
∵PD=x,CD2=y,OP= ![]() AB=4,
AB=4,
∴y=x(4﹣x)=﹣x2+4x.
当点P与点A重合时,x=0;当点P与点B重合时,x=4;
∵点P在大半圆O上运动(点P不与A,B两点重合),
∴0<x<4.
∴y与x之间的函数关系式为y=﹣x2+4x,
自变量x的取值范围是0<x<4.
②当y=3时,﹣x2+4x=3.
解得:x1=1,x2=3.
(i)当x=1时,如图2所示.
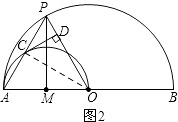
在Rt△CDP中,
∵PD=1,CD= ![]() .
.
∴tan∠CPD= ![]() =
= ![]() ,
,
∴∠CPD=60°.
∵OA=OP,
∴△OAP是等边三角形.
∵AM=OM,
∴PM⊥AO.
∴PM= ![]()
= ![]()
=2 ![]() .
.
(ii)当x=3时,如图3所示.

同理可得:∠CPD=30°.
∵OA=OP,
∴∠OAP=∠APO=30°.
∴∠POB=60°
过点P作PH⊥AB,垂足为H,连接PM,如图3所示.
∵sin∠POH= ![]() =
= ![]() =
= ![]() ,
,
∴PH=2 ![]() .
.
同理:OH=2.
在Rt△MHP中,
∵MH=4,PH=2 ![]() ,
,
∴PM= ![]()
= ![]()
=2 ![]() .
.
综上所述:当y=3时,P,M两点之间的距离为2 ![]() 或2
或2 ![]() .
.
【解析】(1)连接CO、CM,只需证到CD⊥CM.由于CD⊥OP,只需证到CM∥OP,只需证到CM是△AOP的中位线即可.(2)①易证△ODC∽△CDP,从而得到CD2=DPOD,进而得到y与x之间的函数关系式.由于当点P与点A重合时x=0,当点P与点B重合时x=4,点P在大半圆O上运动(点P不与A,B两点重合),因此自变量x的取值范围为0<x<4.②当y=3时,得到﹣x2+4x=3,求出x.根据x的值可求出CD、PD的值,从而求出∠CPD,运用勾股定理等知识就可求出P,M两点之间的距离.
【考点精析】解答此题的关键在于理解平行线的判定与性质的相关知识,掌握由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质,以及对勾股定理的概念的理解,了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.