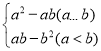题目内容
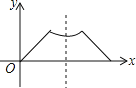
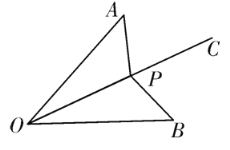
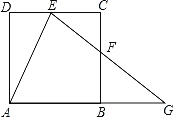
【题目】如图,在正方形ABCD中,点E在DC边上(不与点C,点D重合),点G在AB的延长线上,连结EG,交边BC于点F,且EG=AG,连结AE,AF,设∠AED=![]() ,∠GFB=
,∠GFB=![]() .
.
(1)求![]() ,
,![]() 之间等量关系;
之间等量关系;
(2)若△ADE≌△ABF,AB=2,求BG的长.
【答案】(1)2![]() ﹣
﹣![]() =90°
=90°
(2)![]()
【解析】
(1)由平行线的性质与等腰三角形的性质证明∠AED=∠AEG,再在△BGF中,由三角形的内角和求得![]() 、
、![]() 之间的等量关系;
之间的等量关系;
(2)设BF=x,用x表示EF、FG、BG,进而根据AG=EG列出x的方程求得x便可.
解:(1)∵四边形ABCD是正方形,
∴DC∥AB,∠CBG=∠ABC=90°,
∴∠AED=∠GAE,
∵EG=AG,
∴∠GAE=∠GEA,
∴∠AED=∠AEG=![]() ,
,
∴∠G=180°﹣2![]() ,
,
∵∠BFG+∠G=90°,
∴180°﹣2![]() +
+![]() =90°,
=90°,
∴2![]() ﹣
﹣![]() =90°;
=90°;
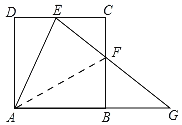
(2)如图,连接AF,∵四边形ABCD是正方形,
∴AB=BC=CD=AD=2,∠C=∠ABC=∠CBG=90°,
设BF=x,
∵△ADE≌△ABF,
∴DE=BF,
∴CE=CF=2﹣x,
∴EF=2![]() x,∠CFE=∠BFG=45°,
x,∠CFE=∠BFG=45°,
∴BG=BF=x,
∴FG=![]() =
=![]() x,
x,
∵AG=EG,
∴2+x=2![]() x+
x+![]() x,
x,
解得,x=2![]() ﹣2,
﹣2,
∴![]() .
.

练习册系列答案
相关题目
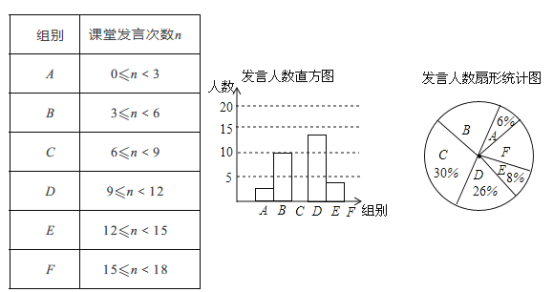
【题目】某学校为了解九年级男同学1000米跑步的成绩,随机抽取了部分男生进行测试,并将测试成绩分为A、B、C、D四个等级,绘制了不完整的成绩等级频数表和扇形统计图.
成绩等级 | 频数 |
A | 24 |
B | 10 |
C | b |
D | 2 |
合计 | a |
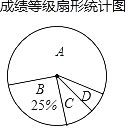
(1)表中a= ,b= ;
(2)扇形图中C的圆心角度数是 ;
(3)若该校共有九年级男生600人,请估计没有获得A等级的学生人数.