Question

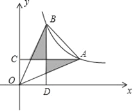
【题目】如图，已知射线OC为∠AOB的平分线，且OA＝OB，点P是射线OC上的任意一点，连接AP、BP．

（1）求证：△AOP≌△BOP；

（2）若∠AOB＝50°，且点P是△AOB的外心，求∠APB的度数；

（3）若∠AOB＝50°，且△OAP为钝角三角形，直接写出∠OAP的取值范围．

Answer 1

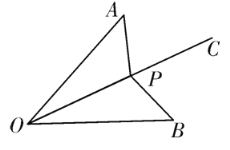
【答案】（1）证明见解析；（2）∠APB＝100°；（3）0°＜∠OAP＜ 65°或90°<∠OAP<155°．

【解析】

（1）根据“SAS”证明即可；

（2）根据三角形外心定义得到PA＝PB＝PO，根据等腰三角形性质和三角形的外角性质求出∠APC＝50°，根据∠APO＝∠BPO即可求解；

（3）根据题意得，分为钝角和为钝角两种情况讨论即可．

解：（1）∵OP平分∠AOB，

∴∠AOP＝∠BOP，

又∵OA＝OB，OP＝OP，

∴△AOP≌△BOP；

（2）∵∠AOB＝50°，

∴∠AOP＝∠BOP＝25°，

∵点P是△AOB的外心，

∴PA＝PB＝PO，

∴∠A＝∠AOP＝25°，

∴∠APC＝∠A＋∠AOP＝50°，

∵△AOP≌△BOP，

∴∠APO＝∠BPO，

∴∠BPC＝∠APC＝50°，

∴∠APB＝100°；

（3）∵∠AOB＝50°，

∴ ，

∴，

∴，

如图1，当为钝角时，

90°<∠OAP<155° ；

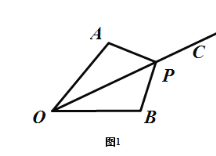
如图2，当为钝角时，

90°<∠OPA<155°，

即90°<<155°，

∴0°＜∠OAP＜ 65°

∴∠OAP的取值范围为：90°<∠OAP<155°或0°＜∠OAP＜ 65°．