题目内容
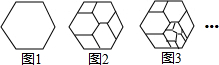
将图1所示的正六边形进行分割得到图2，再将图2中最小的某一个正六边形按同样的方式进行分割得到图3，再将图3中最小的某一个正六边形按同样的方式进行分割…，则第2014个图形中，共有（ ）个正六边形．
| A、4027 | B、6040 | C、10066 | D、以上都不对 |
考点：规律型：图形的变化类
专题：
分析：由图可知，第二个图形有1+3=4个正六边形；第三个图形有1+3+3=7个正六边形；…依此类推，第n个图形中，有1+3（n-1）=3n-2个正六边形．
解答：解：第二个图形有1+3=4个正六边形；
第三个图形有1+3+3=7个正六边形；
…
第n个图形中，有1+3（n-1）=3n-2个正六边形．
第2014个图形中，共有2014×3-2=6040个正六边形．
故选：B．
第三个图形有1+3+3=7个正六边形；
…
第n个图形中，有1+3（n-1）=3n-2个正六边形．
第2014个图形中，共有2014×3-2=6040个正六边形．
故选：B．
点评：本题考查了图形的变化规律：结合图形观察前几个具体数值，即可发现每一次总是多3个正六边形是关键．
练习册系列答案
开心蛙状元测试卷系列答案
相关题目
一水果商某次按一定价格购进一批苹果，销售过程中有20%的苹果正常损耗．则该水果商按一定售价卖完苹果正好不亏不赚，则售价应该在定价基础上加价（本题不考虑税收等其他因素）（ ）
| A、50% | B、40% | C、25% | D、20% |
下面是按照一定规律排列的一列数：
第1个数：
-（1+
）；
第2个数：
-（1+
）×（1+
）×（1+
）；
第3个数：
-（1+
）×（1+
）×（1+
）×（1+
）×（1+
）；
…
依此规律，在第10个数、第11个数、第12个数、第13个数中，最大的数是（ ）
第1个数：
| 1 |
| 2 |
| -1 |
| 2 |
第2个数：
| 1 |
| 3 |
| -1 |
| 2 |
| (-1)2 |
| 3 |
| (-1)3 |
| 4 |
第3个数：
| 1 |
| 4 |
| -1 |
| 2 |
| (-1)2 |
| 3 |
| (-1)3 |
| 4 |
| (-1)4 |
| 5 |
| (-1)5 |
| 6 |
…
依此规律，在第10个数、第11个数、第12个数、第13个数中，最大的数是（ ）
| A、第10个数 |
| B、第11个数 |
| C、第12个数 |
| D、第13个数 |
观察下列图形的构成规律，按此规律，第10个图形中棋子的个数为（ ）
| A、51 | B、45 | C、42 | D、31 |
把边长为1的正方形按如图所示的方式排列，则第n个图形的周长用含n（n为正整数）的式子表示为（ ）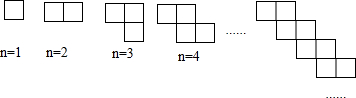
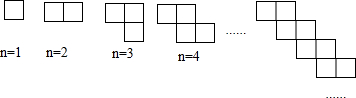
| A、4n | B、2n-2 | C、2n+2 | D、4n-4 |
下列图形都是有同样大小的矩形按一定的规律组成，其中，第①个图形中一共有6个矩形，第②个图形中一共18个矩形，第③图形中一共有36个矩形…则第⑧个图形中矩形的个数为（ ）
| A、126 | B、168 | C、216 | D、372 |
已知代数式|x-3|+|x-7|=4，则下列三条线段不一定能组成三角形的是（ ）
| A、1，x，5 | B、2，x，5 | C、3，x，5 | D、3，x，4 |
一个正方体的表面展开图如图所示，六个面上各有一字，连起来的意思是“预祝中考成功”，把它折成正方体后，与“成”相对的字是（ ）