题目内容
下面是按照一定规律排列的一列数:
第1个数:
-(1+
);
第2个数:
-(1+
)×(1+
)×(1+
);
第3个数:
-(1+
)×(1+
)×(1+
)×(1+
)×(1+
);
…
依此规律,在第10个数、第11个数、第12个数、第13个数中,最大的数是( )
第1个数:
| 1 |
| 2 |
| -1 |
| 2 |
第2个数:
| 1 |
| 3 |
| -1 |
| 2 |
| (-1)2 |
| 3 |
| (-1)3 |
| 4 |
第3个数:
| 1 |
| 4 |
| -1 |
| 2 |
| (-1)2 |
| 3 |
| (-1)3 |
| 4 |
| (-1)4 |
| 5 |
| (-1)5 |
| 6 |
…
依此规律,在第10个数、第11个数、第12个数、第13个数中,最大的数是( )
| A、第10个数 |
| B、第11个数 |
| C、第12个数 |
| D、第13个数 |
考点:规律型:数字的变化类
专题:规律型
分析:通过计算可以发现,第一个数
-
,第二个数为
-
,第三个数为
-
,…第n个数为
-
,由此求第10个数、第11个数、第12个数、第13个数的得数,通过比较得出答案.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| n+1 |
| 1 |
| 2 |
解答:解:第1个数:
-(1+
);
第2个数:
-(1+
)×(1+
)×(1+
);
第3个数:
-(1+
)×(1+
)×(1+
)×(1+
)×(1+
);
…
∴第n个数:
-(1+
)[1+
][1+
]…[1+
]=
-
,
∴第10个数、第11个数、第12个数、第13个数分别为-
,-
,-
,-
,其中最大的数为-
,即第10个数最大.
故选:A.
| 1 |
| 2 |
| -1 |
| 2 |
第2个数:
| 1 |
| 3 |
| -1 |
| 2 |
| (-1)2 |
| 3 |
| (-1)3 |
| 4 |
第3个数:
| 1 |
| 4 |
| -1 |
| 2 |
| (-1)2 |
| 3 |
| (-1)3 |
| 4 |
| (-1)4 |
| 5 |
| (-1)5 |
| 6 |
…
∴第n个数:
| 1 |
| n+1 |
| -1 |
| 2 |
| (-1)2 |
| 3 |
| (-1)3 |
| 4 |
| (-1)2n-1 |
| 2n |
| 1 |
| n+1 |
| 1 |
| 2 |
∴第10个数、第11个数、第12个数、第13个数分别为-
| 9 |
| 22 |
| 5 |
| 12 |
| 11 |
| 26 |
| 3 |
| 7 |
| 9 |
| 22 |
故选:A.
点评:本题考查的是数字的变化类,根据题意找出规律是解答此题的关键.

练习册系列答案
相关题目
用科学记数法表示的数3.61×108,它的原数是( )
| A、361 00 000 000 | B、361 0 000 000 | C、361 000 000 | D、361 00 000 |
下列代数式:-
、
、-
、0、2(x-1)、-32、
;其中整式有( )个.
| 2x |
| 3 |
| xy2-1 |
| 2 |
| x |
| π |
| 1 |
| x |
| A、6 | B、5 | C、4 | D、3 |
下列计算正确的是( )
| A、2a2+a2=3a4 | ||||||
B、
| ||||||
| C、-2(a-1)=2-2a | ||||||
| D、5a+3b=8ab |
将从1开始的正整数按如图方式排列.字母P,Q,M.N表示数字的位置,则2013这个数应排的位置是( )


| A、P | B、N | C、Q | D、M |
有依次排列的3个数:a,b,c,对任意相邻的两个数,都用右边的数减去左边的数,所得之差写在这两个数之间,可产生一个新数串:a,b-a,b,c-b,c,这称为第一次操作;做第二次同样的操作后也可以产生一个新数串:a,b-2a,b-a,a,b,c-2b,c-b,b,c,继续依次操作下去,问:从数串a,b,c,开始操作第10次以后所产生的那个新数串的所有数之和是( )
| A、10a+10b+10c | B、-8a+b+10c | C、9a+10b+11c | D、-9a+b+11c |
将图1所示的正六边形进行分割得到图2,再将图2中最小的某一个正六边形按同样的方式进行分割得到图3,再将图3中最小的某一个正六边形按同样的方式进行分割…,则第2014个图形中,共有( )个正六边形.
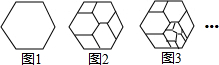

| A、4027 | B、6040 | C、10066 | D、以上都不对 |