题目内容
把边长为1的正方形按如图所示的方式排列,则第n个图形的周长用含n(n为正整数)的式子表示为( )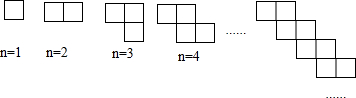
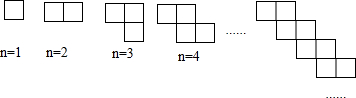
| A、4n | B、2n-2 | C、2n+2 | D、4n-4 |
考点:规律型:图形的变化类
专题:
分析:依次求得n=1,2,3,…,对应的图形的周长,再根据规律以此类推,可得出第n个图形的周长.
解答:解:∵n=1时,周长为4,即4+0×2;
n=2时,周长为6,即4+1×2;
n=3时,周长为8,即4+2×2;
n=4时,周长为10,即4+3×2;
…;
第n个图形周长为4+(n-1)×2=2n+2.
故选:C.
n=2时,周长为6,即4+1×2;
n=3时,周长为8,即4+2×2;
n=4时,周长为10,即4+3×2;
…;
第n个图形周长为4+(n-1)×2=2n+2.
故选:C.
点评:此题考查了平面图形的变化规律,通过观察图形,分析、归纳发现其中的规律,并应用规律解决问题.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
当x=1时,代数式
ax3-3bx+4的值是7,则当x=-1时,这个代数式的值是( )
| 1 |
| 2 |
| A、7 | B、3 | C、1 | D、-7 |
将从1开始的正整数按如图方式排列.字母P,Q,M.N表示数字的位置,则2013这个数应排的位置是( )


| A、P | B、N | C、Q | D、M |
将图①中的正方形剪开得到图②,图②中共有4个正方形;将图②中一个正方形剪开得到图③,图③中共有7个正方形;将图③中一个正方形剪开得到图④,图④中共有10个正方形;…;如此下去,则第2014个图中共有正方形的个数为( )


| A、2014 | B、2017 | C、6040 | D、6044 |
将图1所示的正六边形进行分割得到图2,再将图2中最小的某一个正六边形按同样的方式进行分割得到图3,再将图3中最小的某一个正六边形按同样的方式进行分割…,则第2014个图形中,共有( )个正六边形.
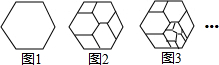

| A、4027 | B、6040 | C、10066 | D、以上都不对 |
如图,它们是用一系列的正方形组合的图形,且图中的三角形都是等腰三角形,第(1)个图形中的正方形边长是1;第(2)个图形中最大的一个正方形的边长为
;第(3)个图形中最大的一个正方形的边长为2;按照此规律,第(8)个图形中最大的一个正方形的边长是( )

| 2 |

A、4
| ||
| B、8 | ||
C、8
| ||
| D、16 |
下列四个式了中,是方程的是( )
| A、1+2+3+4=10 | ||||
| B、2x-3 | ||||
| C、2x=1 | ||||
D、|1-
|
希望中学九年级1班共有学生49人,当该班少一名男生时,男生的人数恰好为女生人数的一半.设该班有男生x人,则下列方程中,正确的是( )
| A、2(x-1)+x=49 | B、2(x+1)+x=49 | C、x-1+2x=49 | D、x+1+2x=49 |
 如图是一个正方体的表面展开图,则原正方体中与“我”字所在的面相对的面上标的字是( )
如图是一个正方体的表面展开图,则原正方体中与“我”字所在的面相对的面上标的字是( )| A、美 | B、丽 | C、射 | D、阳 |