题目内容
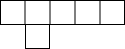
观察下列图形的构成规律，按此规律，第10个图形中棋子的个数为（ ）
| A、51 | B、45 | C、42 | D、31 |
考点：规律型：图形的变化类
专题：
分析：根据图形可分别得出n=1、2、3时，图形中棋子的个数，进而发现规律：第n个图形中棋子的个数为3n+1．
解答：解：n=1时，棋子有4个，4=3×1+1；
n=2时，棋子有7个，7=3×2+1；
n=3时，棋子有10个，10=3×3+1；
…
n=10时，棋子的个数应该是3×10+1=31个．
故选D．
n=2时，棋子有7个，7=3×2+1；
n=3时，棋子有10个，10=3×3+1；
…
n=10时，棋子的个数应该是3×10+1=31个．
故选D．
点评：本题考查了规律型：图形的变化类，关键是通过归纳与总结，得到其中的规律．
练习册系列答案
导学教程高中新课标系列答案
相关题目
某商品先按批发价a元提高10%零售，后又按零售价降低10%出售，则它最后的单价是（ ）元．
| A、a | B、0.99a | C、1.21a | D、0.81a |
有依次排列的3个数：a，b，c，对任意相邻的两个数，都用右边的数减去左边的数，所得之差写在这两个数之间，可产生一个新数串：a，b-a，b，c-b，c，这称为第一次操作；做第二次同样的操作后也可以产生一个新数串：a，b-2a，b-a，a，b，c-2b，c-b，b，c，继续依次操作下去，问：从数串a，b，c，开始操作第10次以后所产生的那个新数串的所有数之和是（ ）
| A、10a+10b+10c | B、-8a+b+10c | C、9a+10b+11c | D、-9a+b+11c |
下列图形都是由同样大小的正方形按一定规律组成的，其中，第1个图形中一共有1个正方形，第2个图形中共有5个正方形，第3个图形中共有14个正方形，…，按照此规律第5个图形中正方形的个数为（ ）
| A、30 | B、46 | C、55 | D、60 |
将图1所示的正六边形进行分割得到图2，再将图2中最小的某一个正六边形按同样的方式进行分割得到图3，再将图3中最小的某一个正六边形按同样的方式进行分割…，则第2014个图形中，共有（ ）个正六边形．
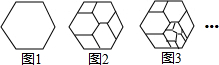
| A、4027 | B、6040 | C、10066 | D、以上都不对 |
如图，图①由3张同样大小的正方形纸片组成，图②由6张同样大小的小正方形纸片组成，图③由10张同样大小的小正方形纸片组成，…，以此规律组成第⑧图需要的同样大小的小正方形纸片张数为（ ）| A、28 | B、36 | C、45 | D、66 |
方程3x-1=2的解是（ ）
| A、x=1 | ||
| B、x=-1 | ||
C、x=-
| ||
D、x=
|
