题目内容
下列图形都是有同样大小的矩形按一定的规律组成，其中，第①个图形中一共有6个矩形，第②个图形中一共18个矩形，第③图形中一共有36个矩形…则第⑧个图形中矩形的个数为（ ）
| A、126 | B、168 | C、216 | D、372 |
考点：规律型：图形的变化类
专题：规律型
分析：由于图①矩形有6个=6×1，图②矩形有18个=6×（2+1），图③矩形有36个=6×（1+2+3），由此即可得到第⑥个图形中矩形的个数．
解答：解：∵第①个图形中一共有6个矩形，第②个图形中一共有18个矩形，第③个图形中一共有36个矩形，…，
∵图①矩形有6个=6×1，
图②矩形有18个=6×（1+2），
图③矩形有36个=6×（1+2+3），
∴第⑧个图形中矩形的个数为：6×（1+2+3+4+5+6+7+8）=216．
故选C．
∵图①矩形有6个=6×1，
图②矩形有18个=6×（1+2），
图③矩形有36个=6×（1+2+3），
∴第⑧个图形中矩形的个数为：6×（1+2+3+4+5+6+7+8）=216．
故选C．
点评：此题主要考查了图形的变化规律，是根据图形进行数字猜想的问题，关键是通过归纳与总结，得到其中的规律，然后利用规律解决一般问题．
练习册系列答案
相关题目
下列代数式：-
、
、-
、0、2（x-1）、-32、
；其中整式有（ ）个．
| 2x |
| 3 |
| xy2-1 |
| 2 |
| x |
| π |
| 1 |
| x |
| A、6 | B、5 | C、4 | D、3 |
有依次排列的3个数：a，b，c，对任意相邻的两个数，都用右边的数减去左边的数，所得之差写在这两个数之间，可产生一个新数串：a，b-a，b，c-b，c，这称为第一次操作；做第二次同样的操作后也可以产生一个新数串：a，b-2a，b-a，a，b，c-2b，c-b，b，c，继续依次操作下去，问：从数串a，b，c，开始操作第10次以后所产生的那个新数串的所有数之和是（ ）
| A、10a+10b+10c | B、-8a+b+10c | C、9a+10b+11c | D、-9a+b+11c |
将图1所示的正六边形进行分割得到图2，再将图2中最小的某一个正六边形按同样的方式进行分割得到图3，再将图3中最小的某一个正六边形按同样的方式进行分割…，则第2014个图形中，共有（ ）个正六边形．
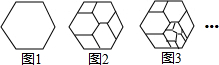
| A、4027 | B、6040 | C、10066 | D、以上都不对 |
如图，图①由3张同样大小的正方形纸片组成，图②由6张同样大小的小正方形纸片组成，图③由10张同样大小的小正方形纸片组成，…，以此规律组成第⑧图需要的同样大小的小正方形纸片张数为（ ）| A、28 | B、36 | C、45 | D、66 |
下列四个式了中，是方程的是（ ）
| A、1+2+3+4=10 | ||||
| B、2x-3 | ||||
| C、2x=1 | ||||
D、|1-
|
方程3x-1=2的解是（ ）
| A、x=1 | ||
| B、x=-1 | ||
C、x=-
| ||
D、x=
|
桌面上有甲、乙、丙三个圆柱形的杯子，杯深均为15公分，各装有10公分高的水，且表记录了甲、乙、丙三个杯子的底面积．今小明将甲、乙两杯内一些水倒入丙杯，过程中水没溢出，使得甲、乙、丙三杯内水的高度比变为3：4：5．若不计杯子厚度，则甲杯内水的高度变为多少公分？（ ）
| 底面积（平方公分） | |
| 甲杯 | 60 |
| 乙杯 | 80 |
| 丙杯 | 100 |
| A、5.4 | B、5.7 |
| C、7.2 | D、7.5 |
如图，经过刨平的木板上的两个点，能弹出一条笔直的墨线，而且只能弹出一条墨线，能解释这一实际应用的数学知识是（ ）| A、两点确定一条直线 | B、两点之间线段最短 | C、垂线段最短 | D、在同一平面内，过一点有且只有一条直线与已知直线垂直 |