题目内容
【题目】若三个非零实数x、y、z满足:只要其中一个数的倒数等于另外两个数的倒数的和,则称这三个实数x、y、z构成“和谐三数组”.
(1)实数1、2、3可以构成“和谐三数组”吗?请说明理由;
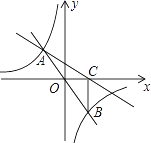
(2)若![]() 三点均在
三点均在![]() (k为常数,k≠0)的图像上,且这三点的纵坐标
(k为常数,k≠0)的图像上,且这三点的纵坐标![]() 构成“和谐三数组”,求实数t的值.
构成“和谐三数组”,求实数t的值.
【答案】(1)不能,理由见解析;(2)![]() 的值为-2或2.
的值为-2或2.
【解析】
![]() 利用和谐三数组的定义进行解答判断即可;
利用和谐三数组的定义进行解答判断即可;
![]() 将M,N,P三点坐标代入反比例函数中,求出
将M,N,P三点坐标代入反比例函数中,求出![]() 、
、![]() 、
、![]() ,进一步求得
,进一步求得![]() ,
,![]() ,
,![]() 的倒数,由和谐三数组分三种情况得到关于t的方程,解方程即可求出t的值.
的倒数,由和谐三数组分三种情况得到关于t的方程,解方程即可求出t的值.
解:![]() 不能,理由如下:
不能,理由如下:
![]() 、2、3的倒数分别为1,
、2、3的倒数分别为1,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() 实数1,2,3不可以构成“和谐三组数”;
实数1,2,3不可以构成“和谐三组数”;![]() ,
,![]() ,
,![]() 三点均在函数
三点均在函数![]() 为常数,
为常数,![]() 的图象上,
的图象上,
![]() 、
、![]() 、
、![]() 均不为0,且
均不为0,且![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() 构成“和谐三组数”,
构成“和谐三组数”,![]() 有以下三种情况:
有以下三种情况:
当![]() 时,则
时,则![]() ,即
,即![]() ,解得
,解得![]() 0(舍去);
0(舍去);
当![]() ,则
,则![]() 即
即![]() ,解得
,解得![]() -2;
-2;
当![]() 时,则
时,则![]() ,即
,即![]() ,解得
,解得![]() 2;
2;
![]() 的值为-2或2.
的值为-2或2.

练习册系列答案
相关题目