题目内容
【题目】已知，如图，长方形ABCD中，AB=3cm，AD=9cm，将此长方形折叠，使点B与点D重合，折痕为EF，则△ABE的面积为( )
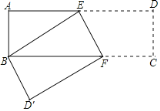
A.6cm2B.8 cm2C.10 cm2D.12 cm2
【答案】A
【解析】
首先根据翻折的性质得到ED＝BE，用AE表示出 ED，BE的长度，然后在Rt△ABE中利用勾股定理求出AE的长度，进而求出AE的长度，就可以利用面积公式求得△ABE的面积了．
解：∵将此长方形折叠，使点B与点D重合，
∴BE=ED．
∵AD=9cm=AE+DE=AE+BE．
∴BE=9﹣AE，
根据勾股定理可知：AB2+AE2=BE2．
∴32+AE2=(9﹣AE)2．
解得：AE=4cm．
∴△ABE的面积为：
×3×4=6(cm2)．
故选：A．
练习册系列答案
相关题目
