题目内容
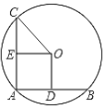
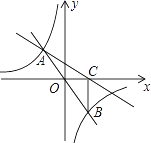
【题目】如图,直线y=mx(m为常数,且m≠0)与双曲线y= ![]() (k为常数,且k≠0)相交于A(﹣2,6),B两点,过点B作BC⊥x轴于点C,连接AC,则△ABC的面积为________.
(k为常数,且k≠0)相交于A(﹣2,6),B两点,过点B作BC⊥x轴于点C,连接AC,则△ABC的面积为________.
【答案】12
【解析】
因为直线与双曲线的交点坐标就是直线解析式与双曲线的解析式联立而成的方程组的解,故求出直线解析式与双曲线的解析式,然后将其联立解方程组,得点B与C的坐标,再根据三角形的面积公式及坐标的意义求解.
解:∵直线y=mx(m为常数,且m≠0)与双曲线y=![]() (k为常数,且k≠0)相交于A(-2,6),
(k为常数,且k≠0)相交于A(-2,6),
∴-2m=6,6=![]() ,
,
∴m=-3,k=-12,
∴直线的解析式为:y=-3x,双曲线的解析式为:y=-![]()
解方程组 得:
得:![]() ,
,![]() ,
,
则点A的坐标为(-2,6),点B的坐标为(2,-6)
∴点C的坐标为(2,0)
∴S△ABC=![]() ×6×(2+2)=12;
×6×(2+2)=12;
故答案为12.

练习册系列答案
 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
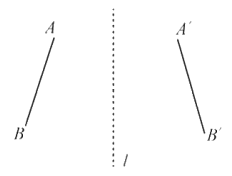
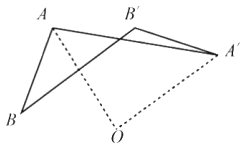
【题目】我们在学完“平移、轴对称、旋转”三种图形的变化后,可以进行进一步研究,请根据示例图形,完成下表.
图形的变化 | 示例图形 | 与对应线段有关的结论 | 与对应点有关的结论 |
平移 |
| (1)__________. |
|
轴对称 |
| (2)__________. | (3)__________. |
旋转 |
|
| (4)__________. |