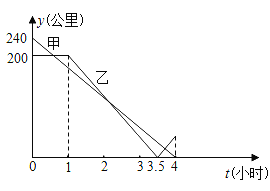
题目内容
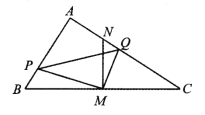
【题目】如图所示,在等边三角形![]() 中,
中,![]() ,射线
,射线![]() ,点
,点![]() 从
从![]() 点出发沿射线
点出发沿射线![]() 以
以![]() 的速度运动,同时点
的速度运动,同时点![]() 从点
从点![]() 出发沿射线
出发沿射线![]() 以
以![]() 的速度运动,设运动时间为
的速度运动,设运动时间为![]() .
.
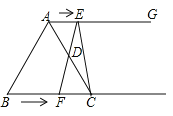
(1)填空:当![]() 为
为 ![]() 时,
时,![]() 是直角三角形;
是直角三角形;
(2)连接![]() ,当
,当![]() 经过
经过![]() 边的中点
边的中点![]() 时,四边形
时,四边形![]() 是否是特殊四边形?请证明你的结论.
是否是特殊四边形?请证明你的结论.
(3)当![]() 为何值时,
为何值时,![]() 的面积是
的面积是![]() 的面积的
的面积的![]() 倍.
倍.
【答案】(1)![]() 或
或![]() ;(2)是平行四边形,见解析;(3)
;(2)是平行四边形,见解析;(3)![]() 或
或![]() .
.
【解析】
(1)根据题意可分两种情况讨论:①当![]() 时,因为
时,因为![]() 是等边三角形,所以
是等边三角形,所以![]() 时满足条件;②当
时满足条件;②当![]() 时,因为
时,因为![]() 是等边三角形,所以
是等边三角形,所以![]() ,得到
,得到![]() ,故
,故![]() ,即可得到答案;
,即可得到答案;
(2)判断出![]() 得出
得出![]() ,即可得出结论;
,即可得出结论;
(3)先判断出![]() 和
和![]() 的边
的边![]() 和
和![]() 上的高相等,进而判断出
上的高相等,进而判断出![]() ,再分两种情况,建立方程求解即可得出结论.
,再分两种情况,建立方程求解即可得出结论.
解:(1)①当![]() 时,
时,
![]()
![]() 是等边三角形,
是等边三角形,![]() ,
,
![]()
![]() ,
,
![]()
![]() 从点
从点![]() 出发沿射线
出发沿射线![]() 以
以![]() 的速度运动,
的速度运动,
![]() 当
当![]() 时,
时,![]() 是直角三角形;
是直角三角形;
②当![]() 时,
时,
![]()
![]() 是等边三角形,
是等边三角形,![]() ,
,
![]()
![]() ,
, ![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]()
![]() 从点
从点![]() 出发沿射线
出发沿射线![]() 以
以![]() 的速度运动,
的速度运动,
![]() 当
当![]() 时,
时,![]() 是直角三角形;
是直角三角形;
故答案为:![]() 或
或![]() ;
;
(2)是平行四边形.
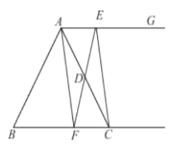
理由:如图,
![]() ,
,
![]() ,
,
![]() 经过
经过![]() 边的中点
边的中点![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() 四边形
四边形![]() 是平行四边形;
是平行四边形;
(3)设平行线![]() 与
与![]() 的距离为
的距离为![]() ,
,
![]() 边
边![]() 上的高为
上的高为![]() ,
,![]() 的边
的边![]() 上的高为
上的高为![]() ,
,
![]() 的面积是
的面积是![]() 的面积的
的面积的![]() 倍,
倍,
![]() ,
,
当点![]() 在线段
在线段![]() 上时,
上时,![]() ,
,
![]() ,
,
![]() ;
;
当点![]() 在
在![]() 的延长线上时,
的延长线上时,![]()
![]() ,
,
![]() ,
,
即:![]() 秒或
秒或![]() 秒时,
秒时,![]() 的面积是
的面积是![]() 的面积的
的面积的![]() 倍,
倍,
故答案为:![]() 或
或![]() .
.

练习册系列答案
相关题目