��Ŀ����
����Ŀ����ƽ��ֱ������ϵxOy�У�������y=mx2��4mx+4m+4��m��0���Ķ���ΪP��P��M�������ԭ��O�����ĶԳƣ�
��1�����P��M�����ꣻ
��2�����������߾���ԭ�㣬�������ߵı���ʽ��
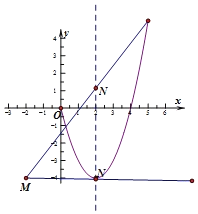
��3���ڣ�2���������£�����������x�ᷭ�ۣ����ۺ��ͼ����0��x��5�IJ��ּ�Ϊͼ��H����NΪ�����߶Գ����ϵ�һ�����㣬����M��N��ֱ����ͼ��H�����������㣬���ͼ�������N��������n��ȡֵ��Χ��
���𰸡���1����P��2��4������M����2����4������2��y=��x2+4x��3����4��n��![]()
����������������1���������߽���ʽת��Ϊ����ʽ���õ�P�����ꣻ��Ϲ���ԭ��ԳƵĵ������д����M�����ꣻ
��2����ԭ����뺯������ʽ���m��ֵ��
��3�����ۺ�����Ϊ![]() ���ͼ����
���ͼ����
��⣺(1)![]()
��P(2,4),��M(2,4)��
(2)��(0,0)���������߱���ʽ��
![]() ,
,
���![]() ,
,
�������߱���ʽΪ��![]()
(3)���ۺ�����Ϊ(2,4)��
��ֱ�߹�(5,5)ʱ�����![]()
����![]()

��ϰ��ϵ�д�
 ���źþ���Ԫ����ĩ��ϵ�д�
���źþ���Ԫ����ĩ��ϵ�д� һ����ʦȨ����ҵ��ϵ�д�
һ����ʦȨ����ҵ��ϵ�д�
�����Ŀ