题目内容
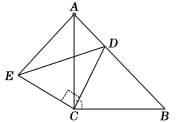
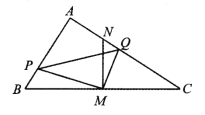
【题目】在△ABC 中,∠BAC=90°,AB<AC,M 是 BC 边的中点,MN⊥BC交 AC 于点 N,动点 P 在线段 BA 上以每秒![]() cm 的速度由点 B 向点 A 运动.同时, 动点 Q 在线段 AC 上由点 N 向点 C 运动,且始终保持 MQ⊥MP. 一个点到终点时,两个点同时停止运动.设运动时间为 t 秒(t>0).
cm 的速度由点 B 向点 A 运动.同时, 动点 Q 在线段 AC 上由点 N 向点 C 运动,且始终保持 MQ⊥MP. 一个点到终点时,两个点同时停止运动.设运动时间为 t 秒(t>0).
(1)△PBM 与△QNM 相似吗?请说明理由;
(2)若∠ABC=60°,AB=4 ![]() cm.
cm.
①求动点 Q 的运动速度;
②设△APQ 的面积为 s(cm2),求 S 与 t 的函数关系式.(不必写出 t 的取值范围)
(3)探求 BP、PQ、CQ 三者之间的数量关系,请说明理由.
【答案】(1) ![]() ;(2)①v=1;②S=
;(2)①v=1;②S=![]() (3)
(3) ![]()
【解析】
(1)由条件可以得出∠BMP=∠NMQ,∠B=∠MNC,就可以得出△PBM∽△QNM;
(2)①根据直角三角形的性质和中垂线的性质BM、MN的值,再由△PBM∽△QNM就可以求出Q的运动速度;
②先由条件表示出AN、AP和AQ,再由三角形的面积公式就可以求出其解析式;
(3)延长QM到D,使MD=MQ,连接PD、BD、BQ、CD,就可以得出四边形BDCQ为平行四边形,再由勾股定理和中垂线的性质就可以得出PQ2=CQ2+BP2.
解:(1)△PBM∽△QNM.
理由:
∵MQ⊥MP,MN⊥BC,
∴∠PMN+∠PMB=90°,∠QMN+∠PMN=90°,
∴∠PMB=∠QMN.
∵∠B+∠C=90°,∠C+∠MNQ=90°,
∴∠B=∠MNQ,
∴△PBM∽△QNM.
(2)∵∠BAC=90°,∠ABC=60°,
∴BC=2AB=8![]() cm.AC=12cm,
cm.AC=12cm,
∵MN垂直平分BC,
∴BM=CM=4![]() cm.
cm.
∵∠C=30°,
∴MN=![]() CM=4cm.
CM=4cm.
①设Q点的运动速度为v(cm/s).
∵△PBM∽△QNM.
∴![]() ,
,
∴![]() ,
,
∴v=1,
答:Q点的运动速度为1cm/s.
②∵AN=AC-NC=12-8=4cm,
∴AP=4![]() -
-![]() t,AQ=4+t,
t,AQ=4+t,
∴S=![]() APAQ=
APAQ=![]() (4
(4![]() -
-![]() t)(4+t)=-
t)(4+t)=-![]() t2+8
t2+8![]() .(0<t≤4)
.(0<t≤4)
当t>4时,AP=-![]() t+4
t+4![]() =(4-t)
=(4-t)![]() .
.
则△APQ的面积为:S=![]() APAQ=
APAQ=![]() (-
(-![]() t+4
t+4![]() )(4+t)=
)(4+t)=![]() t2-8
t2-8![]()
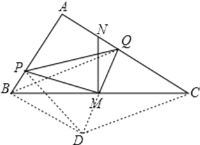
(3)PQ2=CQ2+BP2.
理由:延长QM到D,使MD=MQ,连接PD、BD、BQ、CD,
∵M是BC边的中点,
∴BM=CM,
∴四边形BDCQ是平行四边形,
∴BD∥CQ,BD=CQ.
∴∠BAC+∠ABD=180°.
∵∠BAC=90°,
∴∠ABD=90°,
在Rt△PBD中,由勾股定理得:
PD2=BP2+BD2,
∴PD2=BP2+CQ2.
∵MQ⊥MP,MQ=MD,
∴PQ=PD,
∴PQ2=BP2+CQ2.

 名校课堂系列答案
名校课堂系列答案