Question

如图：∠MON=90°，在∠MON的内部有一个正方形AOCD，点A、C分别在射线OM、ON上，点B₁是ON上的任意一点，在∠MON的内部作正方形AB₁C₁D₁．
（1）连续D₁D，求证：∠D₁DA=90°；
（2）连接CC₁，猜一猜，∠C₁CN的度数是多少？并证明你的结论；
（3）在ON上再任取一点B₂，以AB₂为边，在∠MON的内部作正方形AB₂C₂D₂，观察图形，并结合（1）、（2）的结论，请你再做出一个合理的判断．

Answer 1

（1）证明：∵∠D₁AD+∠B₁AD=90°，∠OAB₁+∠B₁AD=90°，
∴∠B₁AO=∠D₁AD，
∵AD₁=AB₁，AO=AD，
∴△OAB₁≌△DAD₁，∴∠D₁DA=∠O=90°；（D₁，D，C在同一条直线上）．


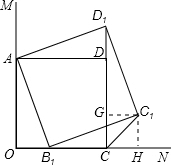
（2）猜想∠C₁CN=45°．
证明：作C₁H⊥ON于H．作C₁G⊥CD₁于G；
则有C₁G=CH．
∵∠C₁D₁C+∠AD₁D=90°，∠C₁B₁H+∠AB₁O=90°
∴∠C₁D₁C=∠C₁B₁H，
∵C₁D₁=B₁C₁，∠D₁C₁E=∠C₁HB₁=90°，
∴△C₁GD₁≌△C₁B₁H，
∴C₁G=C₁H，
又∵CH=C₁G，
∴直角三角形CHC₁是个等腰直角三角形，
∴∠C₁CN=45°．


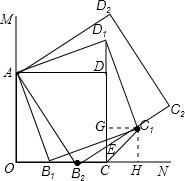
（3）作图；
得∠ADD₂=90°（∠ADD₂=90°、∠C₂CN=45°均可）．