ЬтФПФкШн
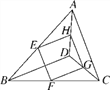
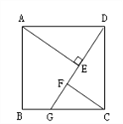
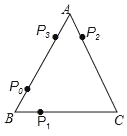
ЁОЬтФПЁПШчЭМЃЌАбДјгажИеыЕФдВаЮзЊХЬAЁЂBЗжБ№ЗжГЩ4ЕШЗнЁЂ3ЕШЗнЕФЩШаЮЧјгђЃЌВЂдкУПвЛИіаЁЧјгђФкБъЩЯЪ§зжЃЈШчЭМЫљЪОЃЉЃЎаЁУїЁЂаЁРжСНИіШЫЭцзЊХЬгЮЯЗЃЌгЮЯЗЙцдђЪЧЃКЭЌЪБзЊЖЏСНИізЊХЬЃЌЕБзЊХЬЭЃжЙЪБЃЌШєжИеыЫљжИСНЧјгђЕФЪ§зжжЎЛ§ЮЊ3ЕФБЖЪ§ЃЌдђаЁУїЪЄЃЛЗёдђЃЌаЁРжЪЄЃЎЃЈШєгажИеыТфдкЗжИюЯпЩЯЃЌдђЮоаЇЃЌашжиаТзЊЖЏзЊХЬЃЉ 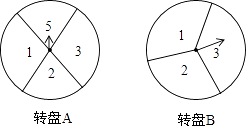
ЃЈ1ЃЉЪдгУСаБэЛђЛЪїзДЭМЕФЗНЗЈЃЌЧѓаЁУїЛёЪЄЕФИХТЪЃЛ
ЃЈ2ЃЉЧыЮЪетИігЮЯЗЙцдђЖдаЁУїЁЂаЁРжЫЋЗНЙЋЦНТ№ЃПзіГіХаЖЯВЂЫЕУїРэгЩЃЎ
ЁОД№АИЁП
ЃЈ1ЃЉНтЃКИљОнЬтвтЛЭМШчЯТЃК
ЙВга12жжЧщПіЃЌжИеыЫљжИСНЧјгђЕФЪ§зжжЎЛ§ЮЊ3ЕФБЖЪ§ЕФга6жжЧщПіЃЌдђаЁУїЪЄЕФИХТЪЪЧ ![]() =
= ![]()
ЃЈ2ЃЉНтЃКгЩЃЈ1ЃЉЕУаЁРжЪЄЕФИХТЪЮЊ1Љ ![]() =
= ![]() ЃЌСНШЫЛёЪЄЕФИХТЪЯрЭЌЃЌЫљвдгЮЯЗЙЋЦН
ЃЌСНШЫЛёЪЄЕФИХТЪЯрЭЌЃЌЫљвдгЮЯЗЙЋЦН
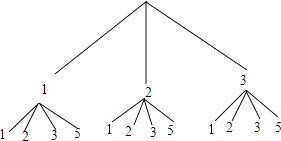
ЁОНтЮіЁПЃЈ1ЃЉСаОйГіЫљгаЧщПіЃЌПДжИеыЫљжИСНЧјгђЕФЪ§зжжЎЛ§ЮЊ3ЕФБЖЪ§ЕФЧщПіеМзмЧщПіЕФЖрЩйЃЌМДПЩЧѓЕУаЁУїЪЄЕФИХТЪЃЛЃЈ2ЃЉгЩЃЈ1ЃЉНјЖјЧѓЕУаЁРжЪЄЕФИХТЪЃЌБШНЯСНИіИХТЪМДПЩЕУГігЮЯЗЪЧЗёЙЋЦНЃЎ
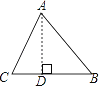
ЁОПМЕуОЋЮіЁПеЦЮеСаБэЗЈгыЪїзДЭМЗЈЪЧНтД№БОЬтЕФИљБОЃЌашвЊжЊЕРЕБвЛДЮЪдбщвЊЩшМЦШ§ИіЛђИќЖрЕФвђЫиЪБЃЌгУСаБэЗЈОЭВЛЗНБуСЫЃЌЮЊСЫВЛжиВЛТЉЕиСаГіЫљгаПЩФмЕФНсЙћЃЌЭЈГЃВЩгУЪїзДЭМЗЈЧѓИХТЪЃЎ

 ЛюСІЪдОэЯЕСаД№АИ
ЛюСІЪдОэЯЕСаД№АИ ПЮПЮгХФмСІХргХ100ЗжЯЕСаД№АИ
ПЮПЮгХФмСІХргХ100ЗжЯЕСаД№АИЁОЬтФПЁПаЁгБКЭаЁКьСНЮЛЭЌбЇдкбЇЯАЁАИХТЪЁБЪБЃЌзіЭЖжРїЛзгЃЈжЪЕиОљдШЕФе§ЗНЬхЃЉЪдбщЃЌЫ§УЧЙВзіСЫ60ДЮЪдбщЃЌЪдбщЕФНсЙћШчЯТЃК
ГЏЩЯЕФЕуЪ§ | 1 | 2 | 3 | 4 | 5 | 6 |
ГіЯжЕФДЮЪ§ | 7 | 9 | 6 | 8 | 20 | 10 |
ЃЈ1ЃЉМЦЫуЁА3ЕуГЏЩЯЁБЕФЦЕТЪКЭЁА5ЕуГЏЩЯЁБЕФЦЕТЪ.
ЃЈ2ЃЉаЁгБЫЕЃКЁАИљОнЩЯЪіЪдбщЃЌвЛДЮЪдбщжаГіЯж5ЕуГЏЩЯЕФИХТЪзюДѓЁБЃЛаЁКьЫЕЃКЁАШчЙћЭЖжР600ДЮЃЌФЧУДГіЯж6ЕуГЏЩЯЕФДЮЪ§е§КУЪЧ100ДЮЁБ.аЁгБКЭаЁКьЕФЫЕЗЈе§ШЗТ№ЃПЮЊЪВУДЃП