题目内容
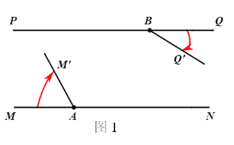
【题目】如图1，直线MN//直线PQ，点A、B分别是直线MN、PQ上的两点．将射线AM绕点A顺时针匀速旋转，射线BQ绕点B顺时针匀速旋转，旋转后的射线分别记为AM′、BQ′，已知射线AM、射线BQ旋转的速度之和为7度/秒．
(1)如果射线BQ 先转动30°后，射线AM、BQ′再同时旋转10秒时，射线AM′与BQ′第一次出现平行．求射线AM、BQ的旋转速度；
(2)若射线AM、BQ分别以（1）中速度同时转动t秒，在射线AM′与AN重合之前，求t为何值时AM′⊥BQ′；
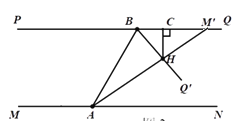
（3）若∠BAN=45°，射线AM、BQ分别以（1）中的速度同时转动t秒，在射线AM′与AN重合之前，射线AM′与BQ′交于点H，过点H作HC⊥PQ，垂足为C，如图2所示，设∠BAH=α，∠BHC=β，求α和β满足的数量关系，直接写出结果．
【答案】(1) 射线AM、BQ的旋转速度分别为5度/秒、2度/秒;(2) 30秒;(3) 当
时，
45°.
【解析】（1）设射线AM、BQ的旋转速度分别为x度/秒、y度/秒，根据速度之和等于7，以及射线AM、BQ的旋转角度相等列方程组求解即可；
（2）根据AM′与BQ′垂直，可得
,求解即可；
（3）根据题意得，延长AM′与BQ交于M′,易得∠A M′B=45°-α,∠HBC=90°-β,而A M′⊥BQ′，从而求得结论.
（1）设射线AM、BQ的旋转速度分别为x度/秒、y度/秒，根据题意得：
,解得
答：射线AM、BQ的旋转速度分别为5度/秒、2度/秒.
（2）由AM′与BQ′垂直，则,
,
答：30秒时AM′⊥BQ′
（3）易得，如图，延长AM′与BQ交于M′,
∵PQ∥MN,
∴∠AM′B=∠N AM′=45°-α,
∵HC⊥PQ,
∴∠HBC=90°-∠BHC=90°-β,
又AM′⊥BQ′,
∴∠HBC+∠AM′B=90°,
∴90°-β+45°-α=90°，即α+β=45°.
