题目内容
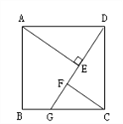
【题目】四边形ABCD是正方形，G是BC上任意一点（点G与B、C不重合），AE⊥DG于E，CF∥AE交DG于F.
（1） 在图中找出一对全等三角形，并加以证明；
（2）求证：AE=FC+EF.
【答案】见解析
【解析】试题分析：（1）图中容易看出△AED≌△DFC．根据两角和其中一角的对边对应相等的两个三角形全等（AAS）可证；
（2）由图中可看出
，从前面全等三角形可得
则可证明．
试题解析：(1)△AED≌△DFC.
证明：∵四边形ABCD是正方形，
又∵AE⊥DG,CF∥AE，
∴∠EAD=∠FDC.
∴△AED≌△DFC(AAS).
(2)证明：∵△AED≌△DFC，
∴AE=DF，ED=FC.
∵DF=DE+EF，
∴AE=FC+EF.
练习册系列答案
相关题目
