��Ŀ����
����Ŀ����ͼ������ABC�У�AB=15��BC=14��AC=13������ABC������� ijѧϰС�龭����������������������Ľ���˼·�����㰴�����ǵĽ���˼·����ɽ����̣�
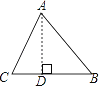
(1)��AD��BC��D����BD=x���ú�x�Ĵ���ʽ��ʾCD����CD=________��
(2)����ݹ��ɶ���������AD��Ϊ���������������̣������x��ֵ��
(3)���ù��ɶ������AD�ij����ټ��������ε������
���𰸡���1��14��x;(2)9����3��84
�������������������1����֪BC=14����BD=x����CD=BC-BD=14-x����2���� Rt��ABD �У����ݹ��ɶ������AD���� Rt��ACD �У����ݹ��ɶ������AD�����������г����̣��ⷽ�̼��ɣ���3���ڣ�2���Ļ��������AD�ij��������������ε������ʽ��⼴��.
���������
��1��CD=(14-x)
��2���� AD �� BC ���ϵĸߣ�
���ABD ����ACD ����ֱ�������Σ�
�� Rt��ABD �У����ݹ��ɶ�����AD=AB-BD=15-x
�� Rt��ACD �У����ݹ��ɶ�������AD=AC-CD=13-��14-x��
��15-x=13-��14-x��
��ã�x=9����BD=9.
��3��AD=15-9=225-81=144����AD=12
����![]()

��ϰ��ϵ�д�
 �����ܾ�ϵ�д�
�����ܾ�ϵ�д� ���ƿ�����ϵ�д�
���ƿ�����ϵ�д� ���¿쳵����������ϵ�д�
���¿쳵����������ϵ�д�
�����Ŀ