题目内容
【题目】如图，抛物线
过
、
两点，点
、
关于抛物线的对称轴对称，过点作
轴，交
轴于点
.
（1）求抛物线的解析式；
（2）直接写出点坐标，并求
的面积；
（3）点
为抛物线上一动点，且位于第四象限，当
面积为6时，求出点坐标；
（4）若点
在直线
上运动，点
在轴上运动，当以、、为顶点的三角形为等腰直角三角形时，直接写出此时点的坐标.
【答案】（1）
；（2）
，3；（3）
；（4）
，
，
，
.
【解析】
（1）把
、
代入
，得到关于a，b的二元一次方程组，求出a，b的值，即可得到抛物线的函数解析式；
（2）根据抛物线的对称性，可得点C的坐标，从而可得BC的值以及BC边上的高，进而求出
的面积；
（3）设
，作
于点
，由
，可列出关于m的方程，进而可求出点P的坐标；
（4）根据以点C，M，N为顶点的三角形为等腰直角三角形，分五类情况讨论，即可求解.
（1）∵抛物线过、两点，
∴
，解得：
∴抛物线的解析式是：.
（2）∵抛物线的解析式是：，
∴抛物线的对称轴是直线x=2，
∵点
、
关于抛物线的对称轴对称，点B的坐标是（1,3），
∴点C的坐标是(3，3)，
∴BC=3-1=2，BC∥x轴，
∴中，BC上的高为3，
∴的面积=2×3÷2=3；
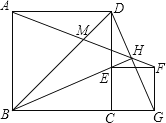
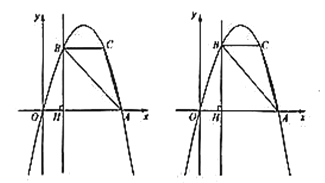
（3）∵点
为抛物线上一动点，且位于第四象限，如图1，
∴设，作于点，
则
，
，
，
∵，
∴
，
即
，
∴
（舍去），
，
∴.
（4）以点C，M，N为顶点的三角形为等腰直角三角形时，分五类情况讨论：
①以点M为直角顶点且M在x轴上方时，如图2，CM=MN，∠CMN=90°，
∵∠CBM=∠MHN=90°，
∴∠BCM+∠BMC=90°，
∵∠HMN+∠BMC=90°，
∴∠BCM=∠HMN，
∴CBMMHN，
∴BC=MH=2，BM=HN=3-2=1，
∴N（2，0）；
②以点M为直角顶点且M在x轴下方时，如图3，
作辅助线，构造如图所示的两直角三角形：RtNEM和RtMDC，同①的证法，
可得：RtNEMRtMDC，
∴EM=CD=5，
∵OH=1，
∴ON=NH-OH=5-1=4，
∴N（-4，0）；
③以点N为直角顶点且N在y轴左侧时，如图4，CN=MN，∠MNC=90°，
作辅助线，构造如图所示的两直角三角形：RtNEM和Rt CDN，同理可得：
RtNEM Rt CDN，
∴ME=NH=DN=3，
∴ON=3-1=2，
∴N（-2，0）；
④以点N为直角顶点且N在y轴右侧时，如图5，CN=MN，∠MNC=90°，
作辅助线，构造如图所示的两直角三角形：RtNEM和Rt CDN，同理可得：
RtNEMRtCDN，
∴ME=DN=NH=3
∴ON=1+3=4，
∴N（4，0）；
⑤以C为直角顶点时，不能构成满足条件的等腰直角三角形；
综上所述：点N的坐标为：，，，.
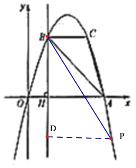
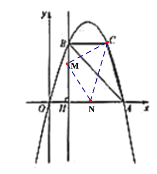
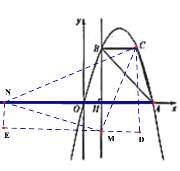
图1 图2 图3
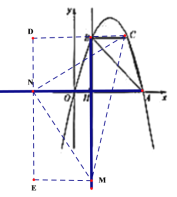
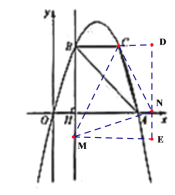
图4 图5
