Question

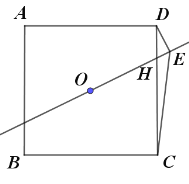
【题目】如图，已知正方形的边长为，点为正方形的中心，点为边上一动点，直线交于点，过点作，垂足为点，连接，则的最小值为（ ）

A.2B.C.D.

Answer 1

【答案】D

【解析】

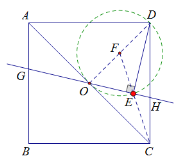
连接OD，AC，取OD中点F，由∠OED=90°可证得点E在以OD中点F为圆心，DF为半径的圆上，进而可知当点C、E、F三点在同一直线上时，CE取最小值，由正方形的性质可得OD=OC=2，进而可得OF=1，最后用勾股定理即可求得CF的长，进而可求得CE的最小值．

解：连接OD，AC，

由题意可知，在正方形中，OD⊥AC，

∵在△ODE中OD的长为定值，∠OED始终为90°，

∴点E在以OD中点F为圆心，OD为直径的圆上，

连接EF，CE，当点C、E、F三点在同一直线上时，CE取最小值，

∵正方形的边长为，点O为正方形中心，

∴，

∴，

∴在Rt△ABC中，，

∴CE的最小值为

故选：D．