题目内容
【题目】如图，在△ABC 中，∠C=90°，BC=3，D，E分别在AB、AC上，将△ADE沿DE翻折后，点A落在点A′处，若A′为CE的中点，则折痕DE的长为（ ）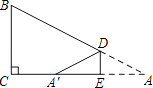
A.
B.3
C.2
D.1
【答案】D
【解析】解：∵△A′DE△ADE翻折而成，
∴AE=A′E，
∵A′为CE的中点，
∴AE=A′E= 
CE，
∴AE= 
AC， 
= ，
∵∠C=90°，DE⊥AC，
∴DE∥BC，
∴△ADE∽△ABC，
∴ 
= 
= ， 
= ，
解得DE=1．
所以答案是：D．
【考点精析】通过灵活运用翻折变换（折叠问题），掌握折叠是一种对称变换，它属于轴对称，对称轴是对应点的连线的垂直平分线，折叠前后图形的形状和大小不变，位置变化，对应边和角相等即可以解答此题．
练习册系列答案
计算高手系列答案
相关题目
