题目内容
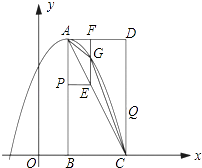
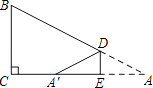
【题目】D，E分别是不等边三角形ABC（即AB≠BC≠AC）的边AB，AC的中点．O是△ABC所在平面上的动点，连接OB，OC，点G，F分别是OB，OC的中点，顺次连接点D，G，F，E．
（1）如图，当点O在△ABC的内部时，求证：四边形DGFE是平行四边形；
（2）若四边形DGFE是菱形，则OA与BC应满足怎样的数量关系？（直接写出答案，不需要说明理由．）
【答案】
（1）证明：∵D、E分别是AB、AC边的中点，
∴DE∥BC，且DE= 
BC，
同理，GF∥BC，且GF= BC，
∴DE∥GF且DE=GF，
∴四边形DEFG是平行四边形
（2）解：当OA=BC时，平行四边形DEFG是菱形
【解析】（1）根据三角形中位线定理，由D、E分别是AB、AC边的中点，得到DE∥BC，且DE= BC，同理，GF∥BC，且GF= BC，得到DE∥GF且DE=GF，根据平行四边形的判定方法得到四边形DEFG是平行四边形；（2）根据一组邻边相等的平行四边形是菱形，当OA=BC时，平行四边形DEFG是菱形.
【考点精析】利用三角形中位线定理和平行四边形的判定对题目进行判断即可得到答案，需要熟知连接三角形两边中点的线段叫做三角形的中位线；三角形中位线定理：三角形的中位线平行于三角形的第三边，且等于第三边的一半；两组对边分别平行的四边形是平行四边形：两组对边分别相等的四边形是平行四边形；一组对边平行且相等的四边形是平行四边形；两组对角分别相等的四边形是平行四边形；对角线互相平分的四边形是平行四边形．
智趣寒假作业云南科技出版社系列答案
【题目】某校对“学生在学校拿手机影响学习的情况”进行了调查，随机调查了部分学生，对此问题的看法分为三种情况：没有影响、影响不大、影响很大，并将调查结果绘制成如下不完整的统计表和扇形统计图，根据统计图表提供的信息，解答下列问题：
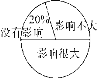
人数统计表如下：
看法 | 没有影响 | 影响不大 | 影响很大 |
学生人数(人) | 20 | 30 | a |
（1）统计表中的a＝ ；
（2）请根据表中的数据，谈谈你的看法（不少于2条）
