题目内容
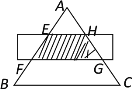
【题目】如图,已知菱形ABCD,对角线AC、BD相交于点O,AC=6,BD=8.点E是AB边上一点,求作矩形EFGH,使得点F、G、H分别落在边BC、CD、AD上.设 AE=m.

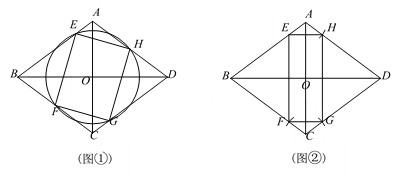
(1)如图①,当m=1时,利用直尺和圆规,作出所有满足条件的矩形EFGH;(保留作图痕迹,不写作法)
(2)写出矩形EFGH的个数及对应的m的取值范围.
【答案】(1)见解析;(2)①当m=0时,存在1个矩形EFGH;②当0<m<![]() 时,存在2个矩形EFGH;③当m=
时,存在2个矩形EFGH;③当m=![]() 时,存在1个矩形EFGH;④当
时,存在1个矩形EFGH;④当![]() <m≤
<m≤![]() 时,存在2个矩形EFGH;⑤当
时,存在2个矩形EFGH;⑤当![]() <m<5时,存在1个矩形EFGH;⑥当m=5时,不存在矩形EFGH.
<m<5时,存在1个矩形EFGH;⑥当m=5时,不存在矩形EFGH.
【解析】
(1)以O点为圆心,OE长为半径画圆,与菱形产生交点,顺次连接圆O与菱形每条边的同侧交点即可;
(2)分别考虑以O为圆心,OE为半径的圆与每条边的线段有几个交点时的情形,共分五种情况.
(1)如图①,如图②(也可以用图①的方法,取⊙O与边BC、CD、AD的另一个交点即可)
(2)∵O到菱形边的距离为![]() ,当⊙O与AB相切时AE=
,当⊙O与AB相切时AE=![]() ,当过点A,C时,⊙O与AB交于A,E两点,此时AE=
,当过点A,C时,⊙O与AB交于A,E两点,此时AE=![]() ×2=
×2=![]() ,根据图像可得如下六种情形:
,根据图像可得如下六种情形:
①当m=0时,如图,存在1个矩形EFGH;

②当0<m<![]() 时,如图,存在2个矩形EFGH;
时,如图,存在2个矩形EFGH;


③当m=![]() 时,如图,存在1个矩形EFGH;
时,如图,存在1个矩形EFGH;
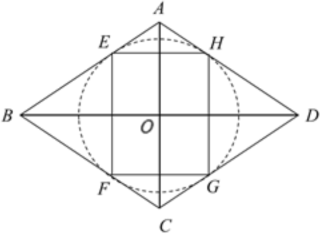
④当![]() <m≤
<m≤![]() 时,如图,存在2个矩形EFGH;
时,如图,存在2个矩形EFGH;

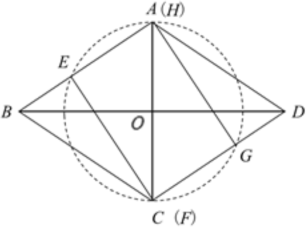
⑤当![]() <m<5时,如图,存在1个矩形EFGH;
<m<5时,如图,存在1个矩形EFGH;

⑥当m=5时,不存在矩形EFGH.

【题目】入学考试前,某语文老师为了了解所任教的甲、乙两班学生假期向的语文基础知识背诵情况,对两个班的学生进行了语文基础知识背诵检测,满分100分.现从两个班分别随机抽取了20名学生的检测成绩进行整理,描述和分析(成绩得分用x表示,共分为五组:
A.0≤x<80,B.80≤x<85,C.85≤x<90,D.90≤x<95,E.95≤x<100),下面给出了部分信息:
甲班20名学生的成绩为:
甲组 | 82 | 85 | 96 | 73 | 91 | 99 | 87 | 91 | 86 | 91 |
87 | 94 | 89 | 96 | 96 | 91 | 100 | 93 | 94 | 99 |
乙班20名学生的成绩在D组中的数据是:93,91,92,94,92,92,92
甲、乙两班抽取的学生成绩数据统计表
班级 | 甲组 | 乙组 |
平均数 | 91 | 92 |
中位数 | 91 | b |
众数 | c | 92 |
方差 | 41.2 | 27.3 |

根据以上信息,解答下列问题:
(1)直接写出上述图表中a,b,c的值:a= ;b= ;c= ;
(2)根据以上数据,你认为甲、乙两个班中哪个班的学生基础知识背诵情况较好?请说明理由(一条理由即可);
(3)若甲、乙两班总人数为125,且都参加了此次基础知识检测,估计此次检测成绩优秀(x≥95)的学生人数是多少?
【题目】某校七年级一班和二班各派出10名学生参加一分钟跳绳比赛,成绩如下表:
跳绳成绩(个) | 132 | 133 | 134 | 135 | 136 | 137 |
一班人数(人) | 1 | 0 | 1 | 5 | 2 | 1 |
二班人数(人) | 0 | 1 | 4 | 1 | 2 | 2 |
(1)两个班级跳绳比赛成绩的众数、中位数、平均数、方差如下表:
众数 | 中位数 | 平均数 | 方差 | |
一班 | a | 135 | 135 | c |
二班 | 134 | b | 135 | 1.8 |
表中数据a= ,b= ,c= ;
(2)请用所学的统计知识,从两个角度比较两个班跳绳比赛的成绩.