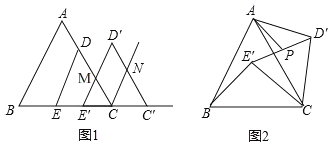Question

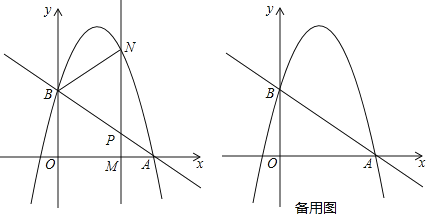
【题目】已知：点P在△ABC内，且满足∠APB=∠APC(如下图)，∠APB+∠BAC=180°，

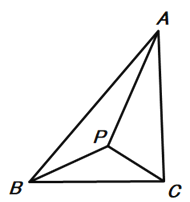
（1）求证：△PAB∽△PCA：

（2）如下图，如果∠APB=120°，∠ABC=90°求的值；

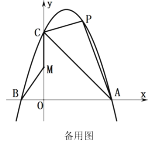
（3）如图，当∠BAC=45°，△ABC为等腰三角形时，求tan∠PBC的值.

Answer 1

【答案】（1）见解析；（2）4；（3）2或或1

【解析】

（1）由已知和等量代换得∠PBA=∠PAC，再根据∠APB=∠APC可证明△PAB∽△PCA

（2）由△PAB∽△PCA可得，通过变形得到，再利用∠APB=120°，∠ABC=90°求出，则可得出的值.

（3）当∠BAC=45°时，可以推出tan∠BPC=，△ABC为等腰三角形，分BA=BC，CA=CB ,AB=AC三种情况，分情况讨论即可.

（1）∵∠APB+∠PBA+∠PBA=180°，∠APB+∠BAC=180°

∴∠BAC=∠PAB+∠PBA

∴∠PBA=∠PAC

∵∠APB=∠APC

∴△PAB∽△PCA

（2）

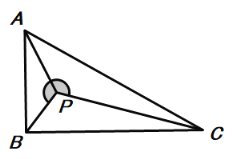
∵△PAB∽△PCA

∴

∴

∵∠APB=120°

∴∠BAC=60°

∵∠ABC=90°

∴

∴

（3）

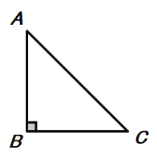
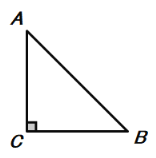
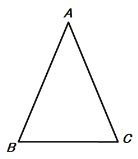
∵∠BAC=45°

∴∠APB=135°=∠APC

∴∠BPC=90°

tan∠BPC=

∵∠BAC=45°，△ABC是等腰三角形

当BA=BC时，由勾股定理可得 ，tan∠BPC=

当CA=CB时，由勾股定理可得 ，tan∠BPC=

当AB=AC 时，tan∠BPC=

综上所述，tan∠PBC=2或或1