ЬтФПФкШн
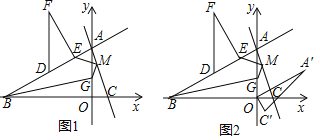
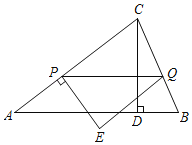
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌABЃНACЃН5ЃЌCDЁЭABгкЕуDЃЌCDЃН3ЃЎЕуPДгЕуAГіЗЂбиЯпЖЮACвдУПУы1ИіЕЅЮЛЕФЫйЖШЯђжеЕуCдЫЖЏЃЎЙ§ЕуPзїPQЁЮABНЛBCгкЕуQЃЌЙ§ЕуPзїACЕФДЙЯпЃЌЙ§ЕуQзїACЕФЦНааЯпЃЌСНЯпНЛгкЕуEЃЎЩшЕуPЕФдЫЖЏЪБМфЮЊtУыЃЎ
ЃЈ1ЃЉЧѓЯпЖЮPQЕФГЄЃЎЃЈгУКЌtЕФДњЪ§ЪНБэЪОЃЉ
ЃЈ2ЃЉЕБЕуEТфдкБпABЩЯЪБЃЌЧѓtЕФжЕЃЎ
ЃЈ3ЃЉЕБЁїPQEгыЁїACDжиЕўВПЗжЭМаЮЪЧЫФБпаЮЪБЃЌжБНгаДГіtЕФШЁжЕЗЖЮЇЃЎ
ЁОД№АИЁПЃЈ1ЃЉPQЃН5ЉtЃЛЃЈ2ЃЉtЃН![]() ЃЛЃЈ3ЃЉ0ЃМtЁм1Лђ
ЃЛЃЈ3ЃЉ0ЃМtЁм1Лђ![]() ЁмtЃМ5
ЁмtЃМ5
ЁОНтЮіЁП
ЃЈ1ЃЉгЩЬтвтЕУГіPCЃНACЉAPЃН5ЉtЃЌгЩPQЁЮABЃЌЕУГіЁїPQCЁзЁїABCЃЌРћгУЯрЫЦШ§НЧаЮЖдгІБпГЩБШР§МДПЩЧѓЕУPQЃН5ЉtЃЛ
ЃЈ2ЃЉЕБЕуEТфдкБпABЩЯЪБЃЌдк![]() жаЃЌЧѓЕУADЃН4ЃЌcosЁЯCADЃН
жаЃЌЧѓЕУADЃН4ЃЌcosЁЯCADЃН![]() ЃЌдк
ЃЌдк![]() жаЃЌcosЁЯCAD
жаЃЌcosЁЯCAD![]() ЃЌЭЦГіAE
ЃЌЭЦГіAE![]() ЃЌгЩPQЁЮABЃЌEQЁЮACЃЌЕУГіЫФБпаЮAEQPЪЧЦНааЫФБпаЮЃЌдђPQЃНAEЃЌМД5ЉtЃН
ЃЌгЩPQЁЮABЃЌEQЁЮACЃЌЕУГіЫФБпаЮAEQPЪЧЦНааЫФБпаЮЃЌдђPQЃНAEЃЌМД5ЉtЃН![]() ЃЌМДПЩЕУГіНсЙћЃЛ
ЃЌМДПЩЕУГіНсЙћЃЛ
ЃЈ3ЃЉЕБЕуEЁЂDЁЂQШ§ЕуЙВЯпЪБЃЌгЩPQЁЮABЃЌEQЁЮACЃЌЕУГіЫФБпаЮADQPЪЧЦНааЫФБпаЮЃЌдђPQЃНADЃН4ЃЌМД5ЉtЃН4ЃЌЕУГіtЃН1ЃЌдђЕБЁїPQEгыЁїACDжиЕўВПЗжЭМаЮЪЧЫФБпаЮЪБЃЌ0ЃМtЁм1ЃЛЕБЕуEТфдкБпABЩЯЪБЃЌгЩЃЈ2ЃЉЕУtЃН![]() ЃЌAEЃНPQЃН
ЃЌAEЃНPQЃН![]() ЃМADЃЌЕУГіЕуPдкЕНДяЕуCЧАЃЌЕуEЪМжедкCDЕФзѓБпЃЌМД
ЃМADЃЌЕУГіЕуPдкЕНДяЕуCЧАЃЌЕуEЪМжедкCDЕФзѓБпЃЌМД![]() ЁмtЃМ5ЃЎ
ЁмtЃМ5ЃЎ
ЃЈ1ЃЉЁпABЃНACЃН5ЃЌЕуPДгЕуAГіЗЂбиЯпЖЮACвдУПУы1ИіЕЅЮЛЕФЫйЖШЯђжеЕуCдЫЖЏЃЌЕуPЕФдЫЖЏЪБМфЮЊtУыЃЌ
ЁрPCЃНACЉAPЃН5ЉtЃЌ
ЁпPQЁЮABЃЌ
ЁрЁїPQCЁзЁїABCЃЌ
Ёр![]()
МДЃК![]()
ЁрPQЃН5ЉtЃЛ
ЃЈ2ЃЉЕБЕуEТфдкБпABЩЯЪБЃЌШчЭМ1ЫљЪОЃК

дкRtЁїACDжаЃЌЁЯADCЃН90ЁуЃЌ
AD![]() ЃЌ
ЃЌ
ЁрcosЁЯCAD![]() ЃЌ
ЃЌ
дкRtЁїAPEжаЃЌЁЯAPEЃН90ЁуЃЌcosЁЯCAD![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрAE![]() AP
AP![]() ЃЌ
ЃЌ
ЁпPQЁЮABЃЌEQЁЮACЃЌ
ЁрЫФБпаЮAEQPЪЧЦНааЫФБпаЮЃЌ
ЁрPQЃНAEЃЌ
МДЃК5ЉtЃН![]() ЃЌ
ЃЌ
НтЕУЃКt![]() ЃЛ
ЃЛ
ЃЈ3ЃЉЕБЕуEЁЂDЁЂQШ§ЕуЙВЯпЪБЃЌШчЭМ2ЫљЪОЃК

ЁпPQЁЮABЃЌEQЁЮACЃЌ
ЁрЫФБпаЮADQPЪЧЦНааЫФБпаЮЃЌ
ЁрPQЃНADЃН4ЃЌ
Ёр5ЉtЃН4ЃЌ
ЁрtЃН1ЃЌ
ЁрЕБЁїPQEгыЁїACDжиЕўВПЗжЭМаЮЪЧЫФБпаЮЪБЃЌ0ЃМtЁм1ЃЛ
ЕБЕуEТфдкБпABЩЯЪБЃЌШчЭМ1ЫљЪОЃЌ
гЩЃЈ2ЃЉЕУЃКt![]() ЃЌ
ЃЌ
AEЃНPQЃН5Љ![]() ЃМADЃЌ
ЃМADЃЌ
ЁрЕуPдкЕНДяЕуCЧАЃЌЕуEЪМжедкCDЕФзѓБпЃЌ
ЁпACЃН5ЃЌ
ЁрtЃМ5ЃЌ
Ёр![]() ЁмtЃМ5ЃЌ
ЁмtЃМ5ЃЌ
злЩЯЃКЕБЁїPQEгыЁїACDжиЕўВПЗжЭМаЮЪЧЫФБпаЮЪБЃЌtЕФШЁжЕЗЖЮЇЮЊ0ЃМtЁм1Лђ![]() ЁмtЃМ5ЃЎ
ЁмtЃМ5ЃЎ