题目内容
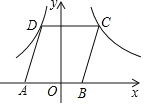
【题目】已知二次函数y=ax2(a≠0)与一次函数y=kx﹣2的图象相交于A、B两点,如图所示,其中A(﹣1,﹣1),
(1)求二次函数和一次函数解析式.
(2)求△OAB的面积.
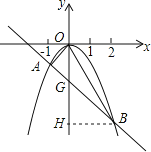
【答案】(1)一次函数表达式为y=﹣x﹣2,二次函数表达式为y=﹣x2,(2)3
【解析】
(1)利用点A的坐标可求出直线与抛物线的解析式;
(2)求出点G的坐标及点B的坐标,利用S△OAB=![]() OG|A的横坐标|+
OG|A的横坐标|+![]() OG点B的横坐标求解即可.
OG点B的横坐标求解即可.
解:(1)∵一次函数y=kx﹣2的图象相过点A(﹣1,﹣1),
∴﹣1=﹣k﹣2,解得k=﹣1,
∴一次函数表达式为y=﹣x﹣2,
∵y=ax2过点A(﹣1,﹣1),
∴﹣1=a×1,解得a=﹣1,
∴二次函数表达式为y=﹣x2,
(2)在y=﹣x﹣2中,令x=0,得y=﹣2,
∴G(0,﹣2),
由一次函数与二次函数联立可得![]() ,
,
解得![]() 或
或![]()
∴点B的坐标为(2,-4)
∴S△OAB=![]() OG|A的横坐标|+
OG|A的横坐标|+![]() OG点B的横坐标=
OG点B的横坐标=![]() ×2×1+
×2×1+![]() ×2×2=1+2=3.
×2×2=1+2=3.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目