Question

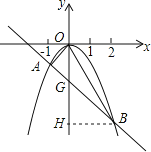
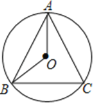
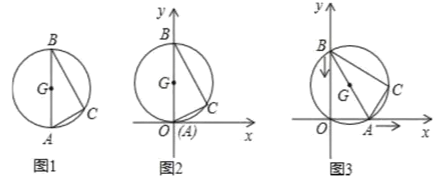
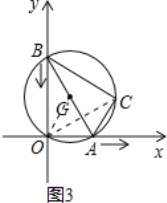
【题目】图1是用钢丝制作的一个几何探究工具，其中△ABC内接于⊙G，AB是⊙G的直径，AB=6，AC=2，现将制作的几何探究工具放在平面直角坐标系中(如图2)，然后点A在射线OX上由点O开始向右滑动，点B在射线OY上也随之向点O滑动(如图3)，当点B滑动至与点O重合时运动结束，在整个运动过程中，点C运动的路径长是( )

A.πB.2πC.4-2D.10-4

Answer 1

【答案】D

【解析】

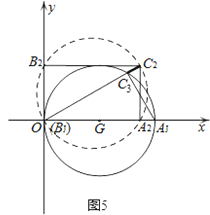
由于在运动过程中，原点O始终在⊙G上，则弧AC的长保持不变，弧AC所对应的圆周角∠AOC保持不变，等于∠XOC，故点C在与x轴夹角为∠ABC的射线上运动．顶点C的运动轨迹应是一条线段，且点C移动到图中C2位置最远，然后又慢慢移动到C3结束，点C经过的路程应是线段C1C2+C2C3．

解：解：如图3，连接OG．
∵∠AOB是直角，G为AB中点，
∴GO=AB=3，
∴原点O始终在⊙G上．
∵∠ACB=90°，AB=6，AC=2，

∴BC=4，

连接OC，则∠AOC=∠ABC，

∴tan∠AOC=，

∴点C在与x轴夹角为∠AOC的射线上运动．
如图4，C1C2=OC2-OC1=6-2=4；
如图5，C2C3=OC2-OC3=6-4；

∴总路径为：C1C2+C2C3=4+6-4=10-4.

故选：D．