题目内容
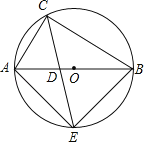
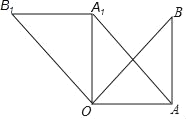
【题目】如图,在Rt△OAB中,∠OAB=90°,OA=AB,将△OAB物点O逆时针方向旋转90°得到△OA1B1.
(1)求∠AOB1的度数;
(2)连结AA1,求证:四边形OAA1B1是平行四边形.
【答案】(1)135°;(2)证明见解析.
【解析】
(1)根据旋转的性质得到∠A1OA=∠B1OB=90°,再由等腰直角三角形的性质得到∠AOB=45°,根据∠AOB1=∠BOB1+∠AOB即可得到结论;
(2)根据旋转的性质得到△OAB≌△OA1B1,∠A1OA=∠B1OB=90°,再根据全等三角形的性质得到AB=A1B1,∠OA1B1=∠OAB=90°,进而可证明OA∥A1B1且相等,即可得出结论.
(1)∵将△OAB物点O逆时针方向旋转90°得到△OA1B1,
∴∠A1OA=∠B1OB=90°.
∵△OAB是等腰直角三角形,
∴∠AOB=45°,
∴∠AOB1=∠BOB1+∠AOB=90°+45°=135°.
(2)∵将△OAB物点O逆时针方向旋转90°得到△OA1B1,
∴△OAB≌△OA1B1,∠A1OA=∠B1OB=90°.
∴AB=A1B1,∠OA1B1=∠OAB=90°,
∴∠AOA1=∠OA1B1=90°,
∴OA∥A1B1.
∵△OAB是等腰直角三角形,
∴OA=AB,
∴OA=AB=A1B1,
∴四边形OAA1B1是平行四边形.

练习册系列答案
相关题目