题目内容
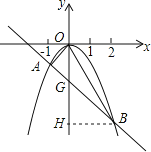
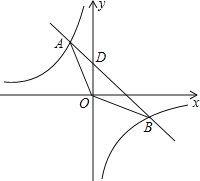
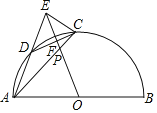
【题目】如图,在以AB为直径的半⊙O上有点C,点D在![]() 上,过圆心作OF⊥CD的于点F,OF、AD的延长线交于点E,连结CE,若∠DEC=90°.
上,过圆心作OF⊥CD的于点F,OF、AD的延长线交于点E,连结CE,若∠DEC=90°.
(1)试说明∠BAC=45°;
(2)若DF=1,△ACE的面积为△DCE面积的3倍,连接AC交OE于点P,求tan∠ACD的值和OP的长;
(3)在(2)的条件下,延长EC与AB的延长线相交于点G,直接写出BG的长 .
【答案】(1)见解析;(2)tan∠ACD=![]() ,OP=
,OP=![]() ;(3)
;(3)![]()
【解析】
(1)连接BC,由垂径定理得出OF垂直平分CD,得出△CDE是等腰直角三角形,∠DCE=∠CDE=45°,由圆内接四边形的性质得出∠ABC=∠CDE=45°,由圆周角定理得出∠ACB=90°,即可得出结论;
(2)连接OC、BD,由题意求出AE=3DE=3![]() ,AD=2
,AD=2![]() ,由勾股定理得出AC=
,由勾股定理得出AC=![]() =2
=2![]() ,由圆周角定理得出∠ACB=∠ADB=90°,得出△ABC是等腰直角三角形,BC=AC=2
,由圆周角定理得出∠ACB=∠ADB=90°,得出△ABC是等腰直角三角形,BC=AC=2![]() ,AB=
,AB=![]() AC=2
AC=2![]() ,得出OC=OA=OB=
,得出OC=OA=OB=![]() ,由勾股定理得出BD=
,由勾股定理得出BD=![]() =4
=4![]() =2AD,再由圆周角定理和三角函数即可得出tan∠ACD=tan∠ABD=
=2AD,再由圆周角定理和三角函数即可得出tan∠ACD=tan∠ABD=![]() =
=![]() ;证明△PCF∽△ABD,得出
;证明△PCF∽△ABD,得出![]() =
=![]() ,求出PF=
,求出PF=![]() ,由勾股定理得出OF=
,由勾股定理得出OF=![]() =3,即可得出OP的长;
=3,即可得出OP的长;
(3)由等腰直角三角形的性质得出OC⊥AB,证明△OCG∽△EAG,得出![]() =
=![]() =
=![]() ,即
,即![]() =
=![]() =
=![]() ,解得:BG=
,解得:BG=![]() ,CG=5
,CG=5![]() 即可.
即可.
(1)证明:连接BC,如图1所示:
∵OF⊥CD,
∴DF=CF,
∴ED=EC,
∵∠DEC=90°,
∴△CDE是等腰直角三角形,
∴∠DCE=∠CDE=45°,
∴∠ABC=∠CDE=45°,
∵AB是直径,
∴∠ACB=90°,
∴∠BAC=45°;
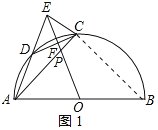
(2)解:连接OC、BD,如图2所示:
∵DF=CF=1,
∴CD=2,△CDE是等腰直角三角形,
∴ED=EC=![]() ,
,
∵△ACE的面积为△DCE面积的3倍,
∴AE=3DE=3![]() ,AD=2
,AD=2![]() ,
,
∴AC=![]() =
=![]() =2
=2![]() ,
,
∵AB是半⊙O的直径,
∴∠ACB=∠ADB=90°,
∵∠BAC=45°,
∴△ABC是等腰直角三角形,
∴BC=AC=2![]() ,AB=
,AB=![]() AC=2
AC=2![]() ,
,
∴OC=OA=OB=![]() ,BD=
,BD=![]() =
=![]() =4
=4![]() =2AD,
=2AD,
∵∠ACD=∠ABD,
∴tan∠ACD=tan∠ABD=![]() =
=![]() ;
;
∵∠PFC=∠ADB=90°,
∴△PCF∽△ABD,
∴![]() =
=![]() ,
,
即![]() =
=![]() ,
,
解得:PF=![]() ,
,
∵OF=![]() =3,
=3,
∴OP=OF﹣PF=![]() ;
;
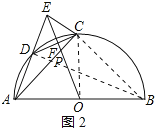
(3)解:如图3所示:
∵△ABC是等腰直角三角形,OA=OB,
∴OC⊥AB,
∴∠COG=90°=∠DEC,
∵∠G=∠G,
∴△OCG∽△EAG,
∴![]() =
=![]() =
=![]() ,
,
即![]() =
=![]() =
=![]() ,
,
解得:BG=![]() ,CG=5
,CG=5![]() ,
,
故答案为:![]() .
.


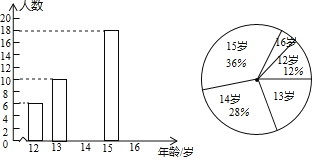
【题目】某校号召全体学生1200人积极参加义工活动,小庆随机抽取部分学生一年中参加义工活动的次数情况进行统计,绘制了如下不完整的统计表和统计图.
次数 | 10 | 8 | 6 | 5 |
人数 | 3 | a | 2 | 1 |
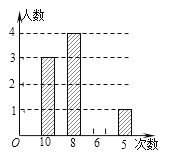
(1)表中数据![]() 为多少?并将条形统计图补充完整;
为多少?并将条形统计图补充完整;
(2)计算被抽取学生平均一年参加义工活动的次数;
(3)估计全校学生中参加义工活动8次的有多少人?