��Ŀ����
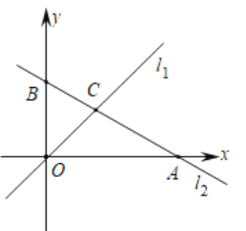
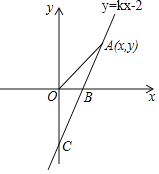
����Ŀ����ͼ��ֱ��y��kx��2��x�ᣬy��ֱ���B��C���㣬����OB��1��
��1����k��ֵ��
��2������A��x��y���ǵ�һ�����ڵ�ֱ��y��kx��2�ϵ�һ�����㣬����A�˶������У���д����AOB�����S��x�ĺ�����ϵʽ��
��3���ڣ�2���������£�̽����
�ٵ���A�˶���ʲôλ��ʱ����AOB�������1��
���ڢٳ���������£�x�����Ƿ����һ��P��ʹ��POA�ǵ��������Σ������ڣ���д����������������P������ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��2����2��S��x��1����3����OA��2![]() ��������P�������ΪP1����2
��������P�������ΪP1����2![]() ��0����P2��2
��0����P2��2![]() ��0����P3��4��0����P4��2��0����
��0����P3��4��0����P4��2��0����
��������
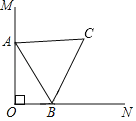
��1����ȷ������B�����꣬���뺯������ʽ�м������k��
��2��������1���ó��ĺ�����ϵʽ�����������ε������ʽ�������������ϵʽ��
��3�������������ε������������A���ꣻ
�������P��m��0������ʾ��AP��OP�������OA��������������ۼ��㼴�ɵó���P���꣮
�⣺��1����OB��1��
��B��1��0����
�ߵ�B��ֱ��y��kx��2�ϣ�
��k��2��0��
��k��2
��2���ɣ�1��֪��k��2��
��ֱ��BC����ʽΪy��2x��2��
�ߵ�A��x��y���ǵ�һ�����ڵ�ֱ��y��2x��2�ϵ�һ�����㣬
��y��2x��2��x��1����
��S��S��AOB��![]() ��OB��|yA|��
��OB��|yA|��![]() ��1��|2x��2|��x��1��
��1��|2x��2|��x��1��
��3������ͼ��

�ɣ�2��֪��S��x��1��
�ߡ�AOB�������1��
��x��2��
��A��2��2����
��OA��2![]() ��
��
�����P��m��0����
��A��2��2����
��OP��|m|��AP��![]() ��
��
�ٵ�OA��OPʱ����2![]() ��|m|����m����2
��|m|����m����2![]() ����P1����2
����P1����2![]() ��0����P2��2
��0����P2��2![]() ��0����
��0����
�ڵ�OA��APʱ����2![]() ��
��![]() ����m��0��m��4����P3��4��0����
����m��0��m��4����P3��4��0����
�۵�OP��APʱ����|m|��![]() ����m��2����P4��2��0����
����m��2����P4��2��0����
������������������P�������ΪP1����2![]() ��0����P2��2
��0����P2��2![]() ��0����P3��4��0����P4��2��0����
��0����P3��4��0����P4��2��0����

 ���Ǽ���С����ϵ�д�
���Ǽ���С����ϵ�д�