题目内容
【题目】如图![]() ,
, ![]() ,
, ![]() ,以
,以![]() 点为顶点、
点为顶点、![]() 为腰在第三象限作等腰
为腰在第三象限作等腰![]() .
.
(![]() )求
)求![]() 点的坐标.
点的坐标.
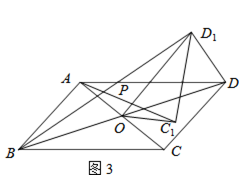
(![]() )如图
)如图![]() ,
, ![]() 为
为![]() 轴负半轴上一个动点,当
轴负半轴上一个动点,当![]() 点沿
点沿![]() 轴负半轴向下运动时,以
轴负半轴向下运动时,以![]() 为顶点,
为顶点, ![]() 为腰作等腰
为腰作等腰![]() ,过
,过![]() 作
作![]() 轴于
轴于![]() 点,求
点,求![]() 的值.
的值.


【答案】(1)点![]() 的坐标为
的坐标为![]() ;(2)
;(2)![]()
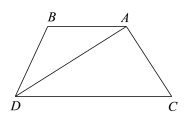
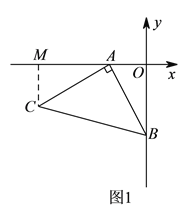
【解析】试题分析:(1)如图1,过C作CM⊥x轴于M点,则可以求出△MAC≌△OBA,可得CM=OA=2,MA=OB=4,即可得到结论;
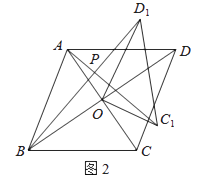
(2)如图2,过D作DQ⊥OP于Q点,则DE=OQ,利用三角形全等的判定定理可得△AOP≌△PQD,进一步可得PQ=OA=2,即OP-DE=2.
试题解析:解:(1)如图1,过C作CM⊥x轴于M点.
∵∠MAC+∠OAB=90°,∠OAB+∠OBA=90°,∴∠MAC=∠OBA.
在△MAC和△OBA中,∵∠CMA=∠AOB=90°,∠MAC=∠OBA,AC=AB,
∴△MAC≌△OBA(AAS),∴CM=OA=2,MA=OB=4,∴OM=OA+AM=2+4=6,∴点C的坐标为(-6,-2).
(2)如图2,过D作DQ⊥OP于Q点,则DE=OQ,∴OP-DE=OP-OQ=PQ.
∵∠APO+∠QPD=90°,∠APO+∠OAP=90°,∴∠QPD=∠OAP.
在△AOP和△PQD中,∵∠AOP=∠PQD=90°,∠OAP=∠QPD,AP=PD,∴△AOP≌△PQD(AAS),∴PQ=OA=2,即OP-DE=2.


练习册系列答案
 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目