��Ŀ����
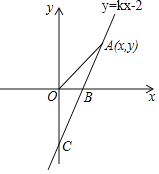
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��l1�Ľ���ʽΪ![]() ��ֱ��l2�Ľ���ʽΪ
��ֱ��l2�Ľ���ʽΪ![]() ����x�ᡢy��ֱ��ڵ�A����B��ֱ��l1��l2���ڵ�C.
����x�ᡢy��ֱ��ڵ�A����B��ֱ��l1��l2���ڵ�C.
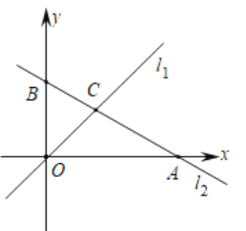

��1�����A����B����C�����꣬�������COB�������
��2����ֱ��l2�ϴ��ڵ�P������B�غϣ�������S��COP=S��COB���������P�����ꣻ
��3����y���Ҳ���һ��ֱ��ƽ����y�ᣬ�ֱ���l1��l2���ڵ�M��N���ҵ�M�ڵ�N���·���y�����Ƿ���ڵ�Q��ʹ��MNQΪ����ֱ�������Σ������ڣ���ֱ��д�����������ĵ�Q�����ꣻ�������ڣ���˵������.
���𰸡���1��A��6��0����B��0��3����C��2��2�������Ϊ3����2��P��4��1������3��Q��0��![]() ����B��0��
����B��0��![]() ����C��0��
����C��0��![]() ��
��
��������
��1����һ�κ�������ʽ�����A��B���꣬��������ʽ�ⷽ����õ���![]() ��Ȼ�����
��Ȼ�����![]() �����
�����![]() �����ɵõ������������
�����ɵõ������������
��2�����![]() ��
��![]() ����
����![]() ����������ϵ������빫ʽ�з��̿ɵ�
����������ϵ������빫ʽ�з��̿ɵ�![]() ��������⣻
��������⣻
��3����![]() ��
��![]() ��
��![]() ����������ֱ�����������ͼ�Σ������߶���ȹ�ϵ�з�����⼴�ɣ�
����������ֱ�����������ͼ�Σ������߶���ȹ�ϵ�з�����⼴�ɣ�
�⣺��1��ֱ��![]() �Ľ���ʽΪ
�Ľ���ʽΪ![]() ��
��
��x=0ʱ��y=3��
��y=0ʱ��![]() ����ã�x=6��
����ã�x=6��
����![]() �ᡢ
�ᡢ![]() ��ֱ��ڵ�
��ֱ��ڵ�![]() ����
����![]() ����ֱ�Ϊ
����ֱ�Ϊ![]() ��
��![]() ��
��
��ֱ��l1��l2���ڵ�C.
�����÷����飺 ����ã�
����ã�![]() ��
��
�ʵ�![]() ��
��
![]() �����
�����![]() ��
��
��2�����![]() ��
��
![]() ����
����![]() ��
��
��![]() ��
��
��ã�![]() ��0����ȥ
��0����ȥ![]() ��
��
�ʵ�![]() ��
��
��3�����![]() ��
��![]() ��
��![]() ������ֱ�Ϊ
������ֱ�Ϊ![]() ��
��![]() ��
��![]() ��
��
����![]() ʱ��
ʱ��
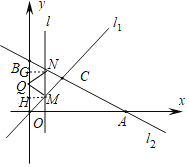
![]() ��
��![]() ��
��![]() ��
��
![]() ��
��![]() ��
��
![]() ��
��
![]() ��
��![]() ��
��
����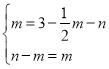 ��
��
��ã� ��
��
��Q��������![]()
����![]() ʱ��
ʱ��
��![]() ������
������![]() ����ã�
����ã�![]() ��
��
![]() ��
��
��Q��������![]()
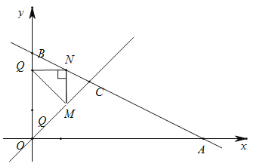
����![]() ʱ��
ʱ��
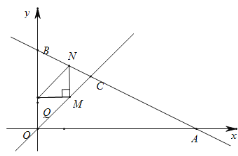
ͬ�����ɵã�![]() ��
��
��Q��������![]()
���ϣ���![]() ������Ϊ
������Ϊ![]() ��
��![]() ��
��![]() ��
��