题目内容
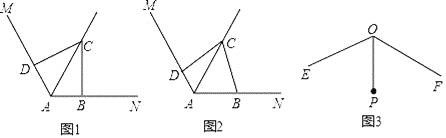
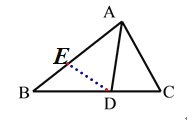
【题目】(10分)如图①,在△ABC中,∠ACB=2∠B,AD为∠BAC的角平分线,
求证:AB=AC+CD
小明同学经过思考,得到如下解题思路:
在AB上截取AE=AC,连接DE,得到△ADE≌△ADC,从而易证AB=AC+CD
(1)请你根据以上解思路写出证明过程;
(2)如图②,若AD为△ABC的外角∠CAE平分线,交BC的延长线于点D,
∠D=25°,其他条件不变,求∠B的度数。


【答案】(1)见解析;(2)50°
【解析】试题分析:先根据“SAS”证明△ADE≌△ADC,从而DE=DC, ∠AED=∠ACB,再由外角的性质可得∠B=∠BDE,从而BE=CD,然后利用等量代换证明结论;(2)利用外角的性质和角平分线的定义得到∠CAD= ![]() ,然后根据三角形内角和列方程求解.
,然后根据三角形内角和列方程求解.
解:(1)∵AD为∠BAC的角平分线,
∴∠BAD=∠CAD.
在△ADE和△ADC中,
∵AC=AE,
∠BAD=∠CAD,
AD=AD,
∴△ADE≌△ADC,
∴DE=DC, ∠AED=∠ACB,
∵∠ACB=2∠B,
∴∠AED=2∠B,
∵∠AED=∠B+∠BDE,
∴∠B=∠BDE,
∴BE=DE,
∴BE=CD.
∵AB=AE+BE,
∴AB=AC+CD.
(2)∵AD为∠BAC的角平分线,
∴∠CAD= ![]() .
.
∵∠ACB=2∠B,
∴∠CAE=∠ACB+∠B=3∠B, ∠BAC=180°-3∠B,
∴∠CAD= ![]() .
.
∴![]() ,
,
解之得
∠B=50°.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案 小学学习好帮手系列答案
小学学习好帮手系列答案
相关题目