题目内容
【题目】如图,将长方形OABC置于平面直角坐标系中,点A的坐标为(0,4),点C的坐标为(m,0)(m>0),点D(m,1)在BC上,将长方形OABC沿AD折叠压平,使点B落在坐标平面内,设点B的对应点为点E.
(1)当m=3时,点B的坐标为_________,点E的坐标为_________;
(2)随着m的变化,试探索:点E能否恰好落在x轴上?若能,请求出m的值;若不能,请说明理由.
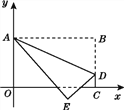
【答案】(1)(3,4),(0,1);(2)点E能恰好落在x轴上,理由见解析.
【解析】试题分析:(1)根据点A、点D、点C的坐标和矩形的性质可以得到点B和点E的坐标;
(2)由折叠的性质求得线段DE和AE的长,然后利用勾股定理得到有关m的方程,求得m的值即可.
试题解析:(1)点B的坐标为(3,4),
∵AB=BD=3,
∴△ABD是等腰直角三角形,
∴∠BAD=45°,
则∠DAE=∠BAD=45°,
则E在y轴上.
AE=AB=BD=3,
∴四边形ABDE是正方形,OE=1,
则点E的坐标为(0,1);
(2)点E能恰好落在x轴上.理由如下:
∵四边形OABC为矩形,
∴BC=OA=4,∠AOC=∠DCE=90°,
由折叠的性质可得:DE=BD=OA-CD=4-1=3,AE=AB=OC=m,
假设点E恰好落在x轴上,在Rt△CDE中,由勾股定理可得EC=![]()
则有OE=OC-CE=m-2![]()
在Rt△AOE中,OA2+OE2=AE2
即42+(m-2![]() )2=m2
)2=m2
解得m=3![]() .
.

练习册系列答案
相关题目