题目内容
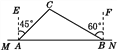
【题目】已知∠MAN=120°，点C是∠MAN的平分线AQ上的一个定点，点B，D分别在AN，AM上，连接BD．
【发现】
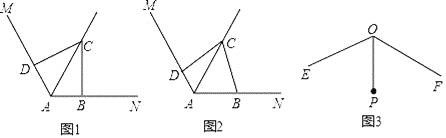
（1）如图1，若∠ABC=∠ADC=90°，则∠BCD= °，△CBD是 三角形；
【探索】
（2）如图2，若∠ABC+∠ADC=180°，请判断△CBD的形状，并证明你的结论；
【应用】
（3）如图3，已知∠EOF=120°，OP平分∠EOF，且OP=1，若点G，H分别在射线OE，OF上，且△PGH为等边三角形，则满足上述条件的△PGH的个数一共有 ．（只填序号）
①2个②3个③4个④4个以上
【答案】（1）60，等边；（2）等边三角形，证明见解析（3）④.
【解析】试题分析：（1）利用四边形的内角和即可得出∠BCD的度数，再利用角平分线的性质定理即可得出CB，即可得出结论；
（2）先判断出∠CDE=∠ABC，进而得出△CDE≌△CFB（AAS），得出CD=CB，再利用四边形的内角和即可得出∠BCD=60°即可得出结论；
（3）先判断出∠POE=∠POF=60°，先构造出等边三角形，找出特点，即可得出结论．
试题解析：（1）如图1，连接BD，
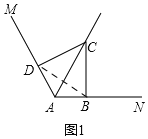
∵∠ABC=∠ADC=90°，∠MAN=120°，
根据四边形的内角和得，∠BCD=360°-（∠ABC+∠ADC+∠MAN）=60°，
∵AC是∠MAN的平分线，CD⊥AM．CB⊥AN，
∴CD=CB，（角平分线的性质定理），
∴△BCD是等边三角形；
故答案为：60，等边；
（2）如图2，同（1）得出，∠BCD=60°（根据三角形的内角和定理），
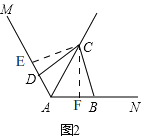
过点C作CE⊥AM于E，CF⊥AN于F，
∵AC是∠MAN的平分线，
∴CE=CF，
∵∠ABC+∠ADC=180°，∠ADC+∠CDE=180°，
∴∠CDE=∠ABC，
在△CDE和△CFB中，
，
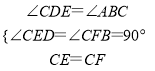∴△CDE≌△CFB（AAS），
∴CD=CB，
∵∠BCD=60°，
∴△CBD是等边三角形；
（3）如图3，
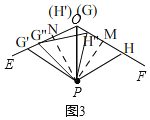
∵OP平分∠EOF，∠EOF=120°，
∴∠POE=∠POF=60°，在OE上截取OG'=OP=1，连接PG'，
∴△G'OP是等边三角形，此时点H'和点O重合，
同理：△OPH是等边三角形，此时点G和点O重合，
将等边△PHG绕点P逆时针旋转到等边△PG'H'，在旋转的过程中，
边PG，PH分别和OE，OF相交（如图中G'，H'）和点P围成的三角形全部是等边三角形，（旋转角的范围为（0°到60°包括0°和60°），
所以有无数个；
理由：同（2）的方法．
故答案为④．
