题目内容
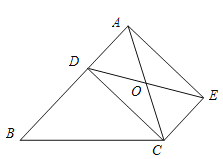
【题目】如图，已知D是△ABC的边AB上一点，CE∥AB，DE交AC于点O，且OA=OC，猜想线段CD与线段AE的大小关系和位置关系，并加以证明．
【答案】详见解析.
【解析】试题分析：根据CE∥AB，可得∠DAO=∠ECO，再由OA=OC，利用ASA可证明△ADO≌△ECO，根据全等三角形的性质可得AD=CE，再根据一组对边平行且相等的四边形是平行四边形即可判定四边形ADCE是平行四边形，由此可得出结论．
试题解析：解：猜想线段CD与线段AE的大小关系和位置关系是：相等且平行．
理由：∵CE∥AB，
∴∠DAO=∠ECO，
∵在△ADO和△ECO中
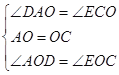
∴△ADO≌△ECO（ASA），
∴AD=CE，
∴四边形ADCE是平行四边形，
∴CD
AE．
练习册系列答案
春雨教育同步作文系列答案
相关题目
