题目内容
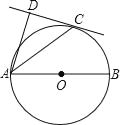
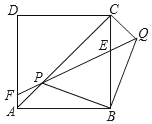
【题目】如图,正方形ABCD、等腰Rt△BPQ的顶点P在对角线AC上(点P与A、C不重合),QP与BC交于E,QP延长线与AD交于点F,连接CQ.
(1)①求证:AP=CQ;②求证:PA2=AFAD;
(2)若AP:PC=1:3,求tan∠CBQ.
【答案】(1)①证明见解析;②证明见解析;(2)![]()
【解析】整体分析:
(1)①用SAS证明△ABP≌△CBQ;②利用①的结论和△EPC与△EBQ组成的”8”字形证明△APF∽△ABP;(2)结合△ABP≌△CBQ,证∠PCQ=90°,由②可得∠CBQ=∠CPQ,又CQ=AP,根据正切的定义即可求解.
(1)①∵四边形ABCD是正方形,∴AB=CB,∠ABC=90°,∴∠ABP+∠PBC=90°,
∵△BPQ是等腰直角三角形,∴BP=BQ,∠PBQ=90°,∴∠PBC+∠CBQ=90°
∴∠ABP=∠CBQ,∴△ABP≌△CBQ,∴AP=CQ;
②∵四边形ABCD是正方形,∴∠DAC=∠BAC=∠ACB=45°,
∵∠PQB=45°,∠CEP=∠QEB,∴∠CBQ=∠CPQ,
由①得△ABP≌△CBQ,∠ABP=∠CBQ
∵∠CPQ=∠APF,∴∠APF=∠ABP,∴△APF∽△ABP,
![]()
(本题也可以连接PD,证△APF∽△ADP)
(2)由①得△ABP≌△CBQ,∴∠BCQ=∠BAC=45°,
∵∠ACB=45°,∴∠PCQ=45°+45°=90°
∴tan∠CPQ=![]() ,
,
由①得AP=CQ,
又AP:PC=1:3,∴tan∠CPQ![]() ,
,
由②得∠CBQ=∠CPQ,
∴tan∠CBQ=tan∠CPQ=![]() .
.

练习册系列答案
相关题目