题目内容
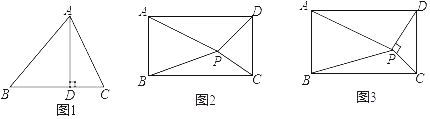
【题目】已知两个共一个顶点的等腰Rt△ABC,Rt△CEF,∠ABC=∠CEF=90°,连接AF,M是AF的中点,连接MB、ME.
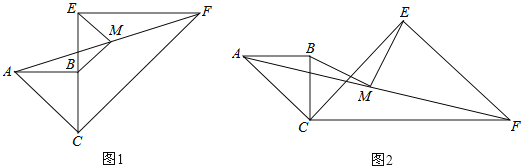
(1)如图1,当CB与CE在同一直线上时,求证:MB∥CF;
(2)如图1,若CB=a,CE=2a,求BM,ME的长;
(3)如图2,当∠BCE=45°时,求证:BM=ME.
【答案】(1)证明见解析;(2)BM=ME=![]() ;(3)证明见解析.
;(3)证明见解析.
【解析】
(1)如图1,延长AB交CF于点D,证明BM为△ADF的中位线即可.
(2)如图2,作辅助线,推出BM、ME是两条中位线.
(3)如图3,作辅助线,推出BM、ME是两条中位线:BM=![]() DF,ME=
DF,ME=![]() AG;然后证明△ACG≌△DCF,得到DF=AG,从而证明BM=ME.
AG;然后证明△ACG≌△DCF,得到DF=AG,从而证明BM=ME.
(1)如图1,延长AB交CF于点D,则易知△ABC与△BCD均为等腰直角三角形,
∴AB=BC=BD.
∴点B为线段AD的中点.
又∵点M为线段AF的中点,
∴BM为△ADF的中位线.
∴BM∥CF.
(2)如图2,延长AB交CF于点D,则易知△BCD与△ABC为等腰直角三角形,
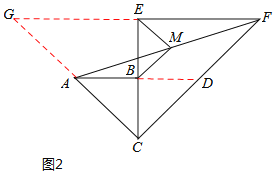
∴AB=BC=BD=a,AC=AD=![]() a,
a,
∴点B为AD中点,又点M为AF中点.
∴BM=![]() DF.
DF.
分别延长FE与CA交于点G,则易知△CEF与△CEG均为等腰直角三角形,
∴CE=EF=GE=2a,CG=CF=![]() a.
a.
∴点E为FG中点,又点M为AF中点.
∴ME=![]() AG.
AG.
∵CG=CF=![]() a,CA=CD=
a,CA=CD=![]() a,∴AG=DF=
a,∴AG=DF=![]() a.
a.
∴BM=ME=![]() .
.
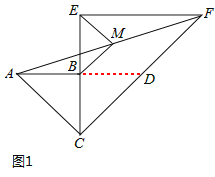
(3)如图3,延长AB交CE于点D,连接DF,则易知△ABC与△BCD均为等腰直角三角形,
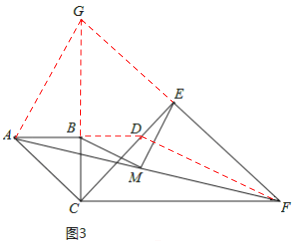
∴AB=BC=BD,AC=CD.
∴点B为AD中点.
又点M为AF中点,∴BM=![]() DF.
DF.
延长FE与CB交于点G,连接AG,则易知△CEF与△CEG均为等腰直角三角形,
∴CE=EF=EG,CF=CG.
∴点E为FG中点.
又点M为AF中点,∴ME=![]() AG.
AG.
在△ACG与△DCF中,∵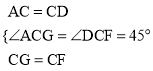 ,
,
∴△ACG≌△DCF(SAS).
∴DF=AG,∴BM=ME.

 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案