Question

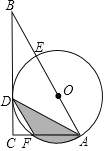
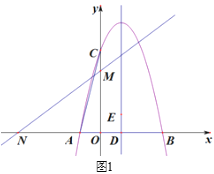
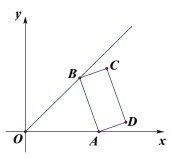
【题目】如图，在平面直角坐标系中，点A，点B分别是x轴正半轴和直线y=x(x>0)上的动点，以AB为边在右侧作矩形ABCD，AB=2，BC=1.

(1)若OA=时，则△ABO的面积是______；

(2)若点A在x轴正半轴移动时，则CO的最大距离是______．

Answer 1

【答案】

【解析】

（1）作BE垂直OA 于E，设OE=m，则BE= m，EA=，在Rt△ABE中利用勾股定理可求得m的值，然后易求得△ABO的面积；

（2）如图作辅助圆和辅助线，根据圆周角定理结合等腰直接三角形的性质可得外接圆半径为，求出HB=HG=1，在Rt△HGC中求出GC=，只有在C、G、共线时，OC最长，求出OC即可.

解：（1）作BE垂直OA 于E，设OE=m，则BE= m，EA=，

在Rt△ABE中，，即：，

解得：，

∴

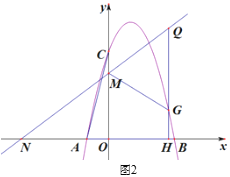
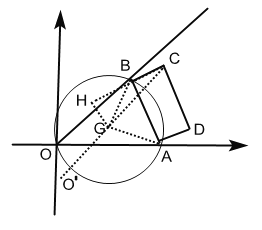
（2）因为AB为定长，∠BOA=45°，作△ABO外接圆G，圆心为G，连接GB、GA、GC、延长GC交圆G于点，

根据题意可知，A、B在运动的过程中可以看作是点O在△ABO外接圆G上运动，

∵∠BOA=45°，∴∠BGA=90°，∠GBC=135°，

作GH⊥CB交其延长线于H，

则∠GBH=∠HGB=45°，

∵AB=2，∴GB=，HB=HG=1，

在Rt△HGC中，GC=，，

只有在C、G、共线时，OC最长，

则.