��Ŀ����
����Ŀ��ijѧУ�ƻ���������ѡ�Σ��������赸���滭���鷨��Ϊ��ǰ�˽�ѧ����ѡ�������ѧУ��ȡ��������ķ��������ʾ����飨ÿ���������ѧ������ѡ�����ֻ��ѡ������һ�ţ����Ե��������������������Ƴ�����������������ͳ��ͼ������ͼ��������Ϣ����������⣺
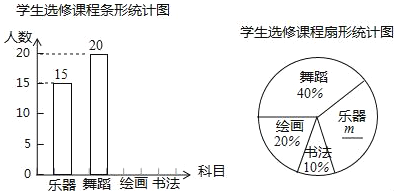
��1�����ε����ѧ������ �ˣ�������ͳ��ͼ�У�m��ֵ�� ��
��2��������ͳ��ͼ����������
��3���ڱ������ѧ���У�ѡ���鷨����2��Ůͬѧ������Ϊ��ͬѧ����Ҫ���������ȡ2��ͬѧ����ѧУ�μ�ij������֯���鷨�����ֱ��д������ȡ��2��ͬѧǡ����1����ͬѧ��1��Ůͬѧ�ĸ��ʣ�
���𰸡���1�����ε����ѧ������50�ˣ�������ͳ��ͼ�У�m��ֵ��30%����2��ͼ����������3��![]() ��
��
��������
�����������1����ѡ�赸�ε�����������ռ���ε����ѧ���������İٷ��ʣ�������ε����ѧ��������Ȼ����ѡ�����ε��������Ա��ε����ѧ�������������������ͳ��ͼ��m��ֵ����2���ñ��ε����ѧ���������˲μӻ滭�Ρ��鷨�ε�����ռ�������İٷ��ʣ�����μӻ滭�Ρ��鷨�ε�������Ȼ����ݲμӻ滭�Ρ��鷨�ε�������������ͳ��ͼ�����������ɣ���3���жϳ��ڱ������ѧ���У�ѡ���鷨����3����ͬѧ��2��Ůͬѧ��Ȼ��Ӧ���б�����д������ȡ��2��ͬѧǡ����1����ͬѧ��1��Ůͬѧ�ĸ��ʼ��ɣ�
�����������1��20��40%=50���ˣ�
15��50=30%
�𣺱��ε����ѧ������50�ˣ�������ͳ��ͼ�У�m��ֵ��30%��
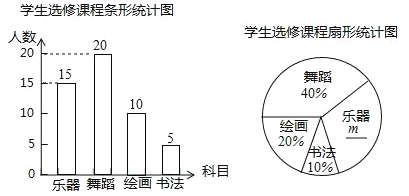
��2��50��20%=10���ˣ�
50��10%=5���ˣ�
 ��
��
��3����5��2=3��������
��ѡ���鷨��5��ͬѧ�У���3����ͬѧ��2��Ůͬѧ��
�� | �� | �� | ٠| ٠| |
�� | / | ���У��У� | ���У��У� | ���У�Ů�� | ���У�Ů�� |
�� | ���У��У� | / | ���У��У� | ���У�Ů�� | ���У�Ů�� |
�� | ���У��У� | ���У��У� | / | ���У�Ů�� | ���У�Ů�� |
Ů | ��Ů���У� | ��Ů���У� | ��Ů���У� | / | ��Ů��Ů�� |
Ů | ��Ů���У� | ��Ů���У� | ��Ů���У� | ��Ů��Ů�� | / |
���еȿ��ܵ������20�֣�����ȡ��2��ͬѧǡ����1����ͬѧ��1��Ůͬѧ�������12�֣�
��P��һ��һŮ��=![]() =
=![]()
������ȡ��2��ͬѧǡ����1����ͬѧ��1��Ůͬѧ�ĸ�����![]() ��
��



