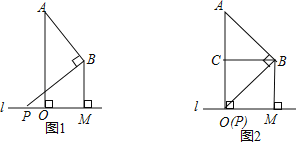题目内容
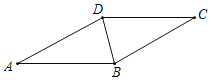
【题目】如图 ![]() ,已知
,已知![]() 中,AB=BC,
中,AB=BC,![]() ,点
,点 ![]() 为斜边
为斜边 ![]() 的中点,连接
的中点,连接 ![]() ,AF是
,AF是 ![]() 的平分线,分别与 BD、
的平分线,分别与 BD、![]() 相交于点 E、F.
相交于点 E、F.

(1)求证:![]() ;
;
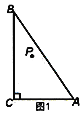
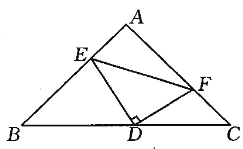
(2)如图![]() ,连接
,连接 ![]() ,在不添加任何辅助线的条件下,直接写出图中所有的等腰三角形(不包含
,在不添加任何辅助线的条件下,直接写出图中所有的等腰三角形(不包含![]() ).
).
【答案】(1)详见解析;(2)(2)△ABD、△CBD 、△ECA、△BEF是等腰三角形
【解析】
(1)根据直角三角形的性质得到BD⊥AC,∠DBC=45°,根据角平分线的定义得到∠BAF=22.5°,根据三角形内角和定理计算,根据等腰三角形的判定定理证明即可;
(2)根据等腰三角形的概念解答.
(1)证明:∠ABC=90,BA=BC,点D为斜边AC的中点,
∴BD⊥AC,∠DBC=45°,
∵AF是∠BAC的平分线,
∴∠BAF=22.5°,
∴∠BFE=67.5°,
∴∠BEF=180°∠EBF∠EFB=67.5°,
∴∠BFE=∠BEF,
∴BE=BF;
(2)∵∠ABC=90°,BA=BC,点D为斜边AC的中点,
∴BD=AD=CD,
∴△ABD、△CBD是等腰三角形,
由已知得,△ABC是等腰三角形,
由(1)得,△BEF是等腰三角形,
∵AF是∠BAC的平分线,BD是∠ABC的平分线,
∴点E是△ABC的内心,
∴∠EAC=∠ECA=22.5°,
∴△AEC是等腰三角形.
∴△ABD、△CBD 、△ECA、△BEF是等腰三角形.

练习册系列答案
相关题目
【题目】某摩托车厂家本周计划每天生产300辆摩托车,由于工厂实行轮休,每天上班人数不一定相等,实际每天生产与计划相比情况如下表:
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减 | ﹣5 | +7 | ﹣3 | +4 | +10 | ﹣9 | ﹣25 |
(1)本周六生产了多少辆摩托车?
(2)本周总产量与计划相比是增加了还是减少了?具体数量是多少?产量最多的一天比产量最少的一天多生产了多少?