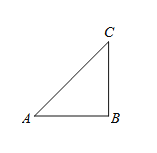Question

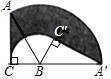
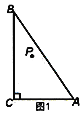
【题目】如图1．在△ABC中，∠ACB＝90°，点P为△ABC内一点．

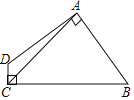
（1）连接PB、PC，将△BCP沿射线CA方向平移，得到△DAE，点B、C、P的对应点分别为点D、A、E，连接CE．

①依题意，请在图2中补全图形；

②如果BP⊥CE，AB＋BP＝9，CE＝，求AB的长．

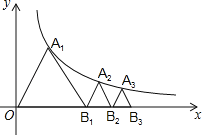
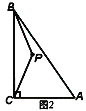
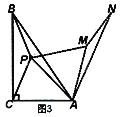
（2）如图3，以点A为旋转中心，将△ABP顺时针旋转60°得到△AMN，连接PA、PB、PC，当AC＝4，AB＝8时，根据此图求PA＋PB＋PC的最小值．

Answer 1

【答案】⑴①见解析，②AB＝6；⑵4.

【解析】（1）①根据题意补全图形即可；

②连接BD、CD．根据平移的性质和∠ACB＝90°，得到四边形BCAD是矩形，从而有CD＝AB，设CD＝AB＝，则PB＝DE＝， 由勾股定理求解即可；

（2）当C、P、M、N四点共线时，PA＋PB＋PC最小．由旋转的性质和勾股定理求解即可．

（1）①补全图形如图所示；

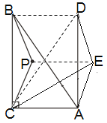
②如图：连接BD、CD．

∵△BCP沿射线CA方向平移，得到△DAE，

∴BC∥AD且BC＝AD，PB＝DE．

∵∠ACB＝90°，

∴四边形BCAD是矩形，∴CD＝AB，设CD＝AB＝，则PB＝，

DE＝BP＝，

∵BP⊥CE，BP∥DE，∴DE⊥CE，

∴，∴，

∴，即AB＝6；

（2）如图，当C、P、M、N四点共线时，PA＋PB＋PC最小．

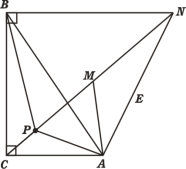
由旋转可得：△AMN≌△APB，∴PB＝MN．

易得△APM、△ABN都是等边三角形，∴PA＝PM，

∴PA＋PB＋PC＝PM＋MN＋PC＝CN，

∴BN＝AB＝8，∠BNA＝60°，∠PAM＝60°，

∴∠CAN＝∠CAB＋∠BAN＝60°＋60°＝120°，

∴∠CBN＝90°．

在Rt△ABC中，易得：，

∴在Rt△BCN中，．