题目内容
【题目】已知:A、B两点在直线l的同一侧,线段AO,BM均是直线l的垂线段,且BM在AO的右边,AO=2BM,将BM沿直线l向右平移,在平移过程中,始终保持∠ABP=90°不变,BP边与直线l相交于点P.
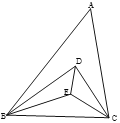
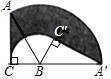
(1)当P与O重合时(如图2所示),设点C是AO的中点,连接BC.求证:四边形OCBM是正方形;
(2)请利用如图1所示的情形,求证:![]() =
=![]() ;
;
(3)若AO=2![]() ,且当MO=2PO时,请直接写出AB和PB的长.
,且当MO=2PO时,请直接写出AB和PB的长.
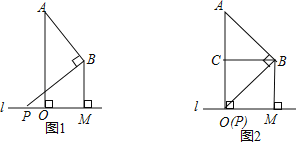
【答案】(1)证明见解析;(2)证明见解析;(3)当点P在O的右侧时, AB=3![]() ,BM=3;点P在O的左侧时,AB=
,BM=3;点P在O的左侧时,AB=![]() ,,PB=
,,PB=![]()
【解析】(1)先证明四边形OCBM是平行四边形,由于∠BMO=90°,所以OCBM是矩形,最后直角三角形斜边上的中线的性质即可证明四边形OCBM是正方形;
(2)连接AP、OB,由于∠ABP=∠AOP=90°,所以A、B、O、P四点共圆,从而利用圆周角定理可证明∠APB=∠OBM,所以△APB∽△OBM,利用相似三角形的性质即可求出答案.
(3)由于点P的位置不确定,故需要分情况进行讨论,共两种情况,第一种情况是点P在O的左侧时,第二种情况是点P在O的右侧时,然后利用四点共圆、相似三角形的判定与性质,勾股定理即可求出答案.
(1)∵2BM=AO,2CO=AO,
∴BM=CO,
∵AO∥BM,
∴四边形OCBM是平行四边形,
∵∠BMO=90°,
∴OCBM是矩形,
∵∠ABP=90°,C是AO的中点,
∴OC=BC,
∴矩形OCBM是正方形;
(2)连接AP、OB,
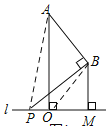
∵∠ABP=∠AOP=90°,
∴A、B、O、P四点共圆,
由圆周角定理可知:∠APB=∠AOB,
∵AO∥BM,
∴∠AOB=∠OBM,
∴∠APB=∠OBM,
∴△APB∽△OBM,
∴![]() ;
;
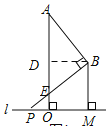
(3)当点P在O的左侧时,如图所示,
过点B作BD⊥AO于点D,
易证△PEO∽△BED,
∴![]() ,
,
易证:四边形DBMO是矩形,
∴BD=MO,OD=BM,
∴MO=2PO=BD,
∴![]() ,
,
∵AO=2BM=2![]() ,
,
∴BM=![]() ,
,
∴OE=![]() ,DE=
,DE=![]() ,
,
易证△ADB∽△ABE,
∴AB2=ADAE,
∵AD=DO=DM=![]() ,
,
∴AE=AD+DE=![]()
∴AB=![]() ,
,
由勾股定理可知:BE=![]() ,
,
易证:△PEO∽△PBM
∴![]() ,
,
∴PB=![]() ;
;
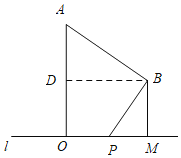
当点P在O的右侧时,如图所示,
过点B作BD⊥OA于点D,
∵MO=2PO,
∴点P是OM的中点,
设PM=x,BD=2x,
∵∠AOM=∠ABP=90°,
∴A、O、P、B四点共圆,
∴四边形AOPB是圆内接四边形,
∴∠BPM=∠A,
∴△ABD∽△PBM,
∴![]() ,
,
又易证四边形ODBM是矩形,AO=2BM,
∴AD=BM=![]() ,
,
∴![]() ,
,
解得:x=![]() ,
,
∴BD=2x=2![]()
由勾股定理可知:AB=3![]() ,BM=3.
,BM=3.

 全能测控期末小状元系列答案
全能测控期末小状元系列答案