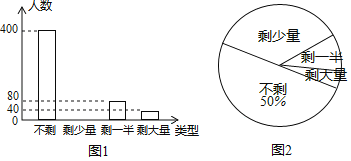
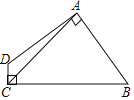
题目内容
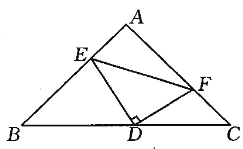
【题目】如图,在等腰直角△ABC中,AB=AC,点D是斜边BC的中点,点E、F分别是AB、AC边上的点,且DE⊥DF.
(1)证明:BE+CF=EF2;
(2)若BE=12,CF=5,求△DEF的面积.
【答案】(1)见解析;(2)![]()
【解析】
(1)连接AD,首先利用等腰直角三角形的性质得到AD⊥BC,AD=CD=BD,∠C=∠DAE,得出∠CDF=∠ADE,然后利用ASA证得DCF≌△ADE,得出CF=AE,DF=DE,得出BE=AF,再根据勾股定理即可得出结论;
(2)由(1)知:AE=CF,AF=BC,DE=DF,即△EDF为等腰直角三角形,在Rt△AEF中,运用勾股定理求出EF,进而求出DE、DF的值,代入S△EDF=![]() DE2进行求解即可.
DE2进行求解即可.
(1)证明:连接AD,如图所示:

∵AB=AC,D为BC的中点,∠BAC=90°,
∴AD⊥BC,AD=CD=BD,∠C=∠B=45°,∠DAE=45°,
∵DE⊥DF,
∴∠CDF+∠ADF=∠EDA+∠ADF,
即∠CDF=∠ADE,
在△DCF和△ADE中,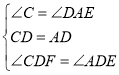 ,
,
∴△DCF≌△ADE(ASA),
∴CF=AE,DF=DE,
∴BE=AF,
∵AF2+AE2=EF2,
∴BE2+CF2=EF2;
(2)由(1)知:AE=CF=5,同理AF=BE=12,
∵∠EAF=90°,
∴EF2=AE2+AF2=52+122=169,
∴EF=13,
又∵由(1)知:△AED≌△CFD,
∴DE=DF,
∴△DEF为等腰直角三角形,
∴DE=DF=EF![]() ,
,
∴△DEF的面积=![]() DE2=
DE2=![]() .
.

【题目】问题背景:
小红同学在学习过程中遇到这样一道计算题“计算![]() ”,他觉得太麻烦,估计应该有可以简化计算的方法,就去请教崔老师.崔老师说:你完成下面的问题后就可能知道该如何简化计算啦!
”,他觉得太麻烦,估计应该有可以简化计算的方法,就去请教崔老师.崔老师说:你完成下面的问题后就可能知道该如何简化计算啦!
获取新知:
请你和小红一起完成崔老师提供的问题:
(1)填写下表:
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
(2)观察表格,你发现![]() 与
与![]() 有什么数量关系?请直接写出
有什么数量关系?请直接写出![]() 与
与![]() 之间的数量关系.
之间的数量关系.
解决问题:
(3)请结合上述的有关信息,计算![]() .
.