��Ŀ����
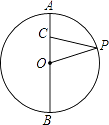
����Ŀ����֪��ƽ��ֱ������ϵxOy�У�O������ԭ�㣬��P��1��1��ΪԲ�ĵġ�P��x�ᣬy��ֱ������ڵ�M�͵�N����F�ӵ�M��������x����������ÿ��1����λ���ȵ��ٶ��˶�������PF������P��PE��PF��y���ڵ�E�����F�˶���ʱ����t�루t��0���� 
��1������E��y��ĸ������ϣ���ͼ��ʾ������֤��PE=PF��
��2���ڵ�F�˶������У���OE=a��OF=b�����ú�a�Ĵ���ʽ��ʾb��
��3������F���ڵ�M�ĶԳƵ�F�䣬����M��E��F������������ߵĶԳ��ύx���ڵ�Q������QE���ڵ�F�˶������У��Ƿ����ijһʱ�̣�ʹ���Ե�Q��O��EΪ��������������Ե�P��M��FΪ��������������ƣ������ڣ���ֱ��д��t��ֵ���������ڣ���˵�����ɣ�
���𰸡�
��1��֤������ͼ������PM��PN��
�ߡ�P��x�ᣬy��ֱ������ڵ�M�͵�N��
��PM��MF��PN��ON��PM=PN��
���PMF=��PNE=90���ҡ�NPM=90�㣬
��PE��PF��
��NPE=��MPF=90�㩁��MPE��
�ڡ�PMF�͡�PNE�У�
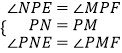 ��
��
���PMF�ա�PNE��ASA����
��PE=PF
��2��֤�����⣺�����������
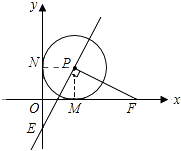
�ٵ�t��1ʱ����E��y��ĸ������ϣ���ͼ1��
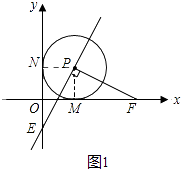
�ɣ�1���á�PMF�ա�PNE��
��NE=MF=t��PM=PN=1��
��b=OF=OM+MF=1+t��a=NE��ON=t��1��
��b��a=1+t����t��1��=2��
��b=2+a��
��0��t��1ʱ����ͼ2����E��y����������ԭ���ϣ�
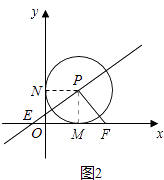
ͬ����֤��PMF�ա�PNE��
��b=OF=OM+MF=1+t��a=OE=ON��NE=1��t��
��b+a=1+t+1��t=2��
��b=2��a��
������������t��1ʱ��b=2+a����0��t��1ʱ��b=2��a��
��3��֤�������ڣ�
����ͼ3����0��t��1ʱ��
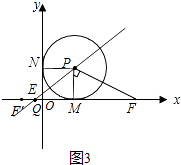
��F��1+t��0����F��F����ڵ�M�Գƣ�M������Ϊ��1��0����
��F�䣨1��t��0��
�߾���M��E��F������������ߵĶԳ��ύx���ڵ�Q��
��Q��1�� ![]() t��0��
t��0��
��OQ=1�� ![]() t��
t��
�ɣ�1���á�PMF�ա�PNE
��NE=MF=t��
��OE=1��t��
����OEQ�ס�MPF
�� ![]()
�� ![]() =
= ![]() ����ʱ�⣬
����ʱ�⣬
����OEQ�ס�MFPʱ��
�� ![]() ��
��
![]() =
= ![]() ��
��
��ã�t=2�� ![]() ��t=2+
��t=2+ ![]() ����ȥ����
����ȥ����
����ͼ4����1��t��2ʱ��
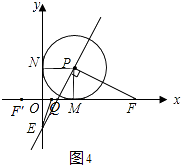
��F��1+t��0����F��F����ڵ�M�Գƣ�M������Ϊ��1��0����
��F�䣨1��t��0��
�߾���M��E��F������������ߵĶԳ��ύx���ڵ�Q��
��Q��1�� ![]() t��0��
t��0��
��OQ=1�� ![]() t��
t��
�ɣ�1���á�PMF�ա�PNE
��NE=MF=t��
��OE=t��1
����OEQ�ס�MPF
�� ![]()
�� ![]() =
= ![]() ��
��
��ã�t= ![]() ��
��
����OEQ�ס�MFPʱ��
�� ![]() ��
��
![]() =
= ![]() ��
��
��ã�t= ![]() ��
��
����ͼ5����t��2ʱ��
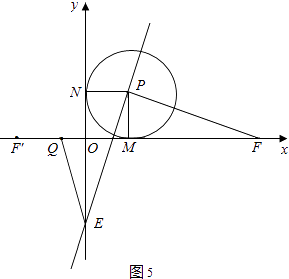
��F��1+t��0����F��F����ڵ�M�Գƣ�
��F�䣨1��t��0��
�߾���M��E��F������������ߵĶԳ��ύx���ڵ�Q��
��Q��1�� ![]() t��0��
t��0��
��OQ= ![]() t��1��
t��1��
�ɣ�1���á�PMF�ա�PNE
��NE=MF=t��
��OE=t��1
����OEQ�ס�MPF
�� ![]()
�� ![]() =
= ![]() ��
��
�⣬
����OEQ�ס�MFPʱ��
�� ![]() ��
��
![]() =
= ![]() ��
��
��ã�t=2+ ![]() ��t=2��
��t=2�� ![]() ����ȥ��
����ȥ��
���Ե�t=2�� ![]() ��
�� ![]() ��
�� ![]() ��t=2+
��t=2+ ![]() ʱ��ʹ���Ե�Q��O��EΪ��������������Ե�P��M��FΪ���������������
ʱ��ʹ���Ե�Q��O��EΪ��������������Ե�P��M��FΪ���������������
����������1������PM��PN�����á�PMF�ա�PNE֤������2��������������ٵ�t��1ʱ����E��y��ĸ������ϣ��ڵ�0��t��1ʱ����E��y����������ԭ���ϣ��ٸ��ݣ�1����⣬��3���������������1��t��2ʱ����t��2ʱ������������ʱ������������������ݱ���ʽ���ʱ��t��

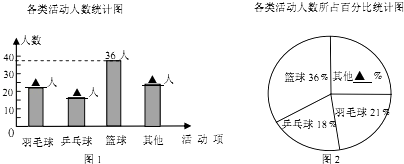
����Ŀ��ijУΪ���˽�ѧ��Т����ĸ�������ѡ�A��Ϊ��ĸϴһ�νţ�B���︸ĸ��һ�μ���C������ĸ��һ�����D������������ȫУ��Χ�������ȡ��������ѧ�����е��飬�õ���ͼ����������Ϣδ��������ѧ��Т����ĸ���ͳ�Ʊ���
ѡ�� | Ƶ�� | Ƶ�� |
A | m | 0.15 |
B | 60 | p |
C | n | 0.4 |
D | 48 | 0.2 |
����������Ϣ����������⣺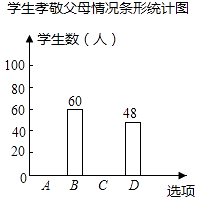
��1����α������ѧ���ж����ˣ�
��2�������m��n��p��ֵ������ȫ����ͳ��ͼ��
��3����У��1600��ѧ�������Ƹ�Уȫ��ѧ����ѡ��Bѡ����ж����ˣ�